Zadanie nr 2355016
Trójkąt 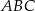 jest ostrokątny oraz
jest ostrokątny oraz 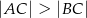 . Dwusieczna
. Dwusieczna 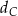 kąta
kąta 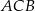 przecina bok
przecina bok 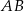 w punkcie
w punkcie 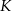 . Punkt
. Punkt 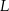 jest obrazem punktu
jest obrazem punktu 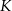 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 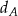 kąta
kąta 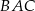 , punkt
, punkt 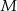 jest obrazem punktu
jest obrazem punktu 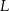 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 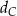 kąta
kąta 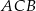 , a punkt
, a punkt 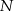 jest obrazem punktu
jest obrazem punktu 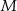 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 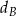 kąta
kąta 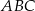 (zobacz rysunek).
(zobacz rysunek).
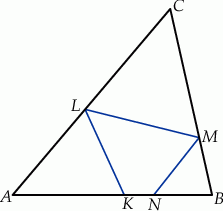
Udowodnij, że na czworokącie 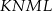 można opisać okrąg.
można opisać okrąg.
Rozwiązanie
Dorysujmy dwusieczne 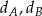 i
i 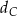 .
.
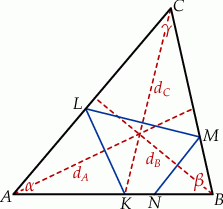
W każdym z trójkątów 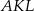 ,
, 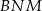 i
i 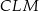 dwusieczna pokrywa się z wysokością, więc są to trójkąty równoramienne (każdy z nich ma oś symetrii). Jeżeli więc oznaczymy
dwusieczna pokrywa się z wysokością, więc są to trójkąty równoramienne (każdy z nich ma oś symetrii). Jeżeli więc oznaczymy 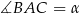 ,
, 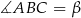 i
i 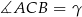 , to
, to
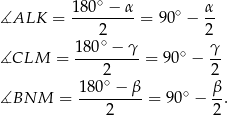
Stąd
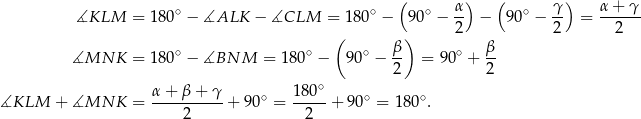
To oznacza, że rzeczywiście na czworokącie 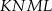 można opisać okrąg.
można opisać okrąg.

