Zadanie nr 4979382
Dany jest trójkąt 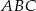 . Odcinek
. Odcinek 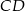 jest wysokością tego trójkąta, punkt
jest wysokością tego trójkąta, punkt 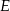 jest środkiem boku
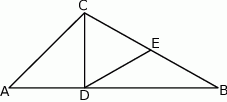
jest środkiem boku 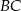 (tak jak na rysunku) i
(tak jak na rysunku) i 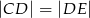 . Udowodnij, że trójkąt
. Udowodnij, że trójkąt 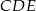 jest równoboczny.
jest równoboczny.
Rozwiązanie
Sposób I
Zauważmy, że z podanych informacji wynika, że odcinek 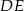 jest środkową w trójkącie prostokątnym
jest środkową w trójkącie prostokątnym 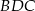 . Ponieważ środek
. Ponieważ środek 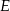 przeciwprostokątnej
przeciwprostokątnej 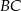 tego trójkąta jest środkiem okręgu opisanego na trójkącie
tego trójkąta jest środkiem okręgu opisanego na trójkącie 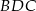 , mamy
, mamy
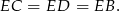
Ponadto z założenia 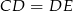 , więc trójkąt
, więc trójkąt 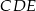 jest rzeczywiście równoboczny.
jest rzeczywiście równoboczny.
Sposób II
Tym razem dorysujmy odcinek 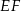 prostopadły do
prostopadły do 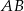 .
.
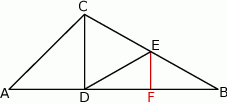
Zauważmy, że z założenia
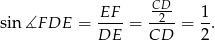
Zatem 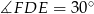 i
i
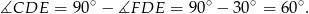
To z kolei oznacza, że trójkąt 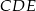 jest równoramienny z kątem między ramionami równym
jest równoramienny z kątem między ramionami równym 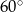 . Jest to więc trójkąt równoboczny.
. Jest to więc trójkąt równoboczny.

