Zadania.info Największy internetowy zbiór zadań z matematyki

/Konkursy/Zadania/Geometria/Planimetria/Trapez

Wyszukiwanie zadań

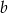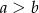Podstawy trapezu mają długości a i b (a > b ). Suma miar kątów wewnętrznych przy dłuższej podstawie wynosi 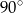90∘ . Oblicz długość odcinka łączącego środki podstaw trapezu.

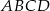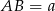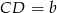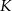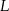Podstawy trapezu ABCD mają długości AB = a i CD = b . Na ramionach trapezu wybrano punkty K i L w ten sposób, że odcinek 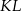KL jest równoległy do podstaw oraz 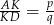AKKD- = pq . Oblicz długość odcinka KL .

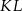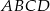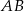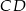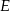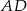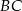W trapezie ABCD podstawa AB jest 3 razy dłuższa od podstawy CD . Przekątne tego trapezu przecinają się w punkcie E , a proste zawierające ramiona AD i BC przecinają się w punkcie 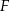F . Oblicz stosunek pola czworokąta 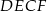DECF do pola trapezu ABCD .

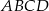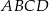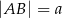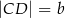Podstawy trapezu ABCD mają długości |AB | = a i |CD | = b , przy czym 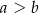a > b . Udowodnij, że odcinek łączący środki przekątnych tego trapezu ma długość a−b- 2 .

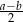Podstawy trapezu mają długości 9 i 12. Oblicz długość odcinka łączącego środki przekątnych tego trapezu.

Ramiona trapezu są średnicami dwóch okręgów. Wykaż, że jeśli okręgi te są styczne zewnętrznie, to w trapez ten można wpisać okrąg.

Udowodnij, że średnica okręgu wpisanego w trapez równoramienny, ma długość równą średniej geometrycznej długości podstaw trapezu.

Ukryj Podobne zadania

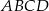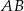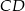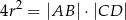Trapez równoramienny ABCD o podstawach AB i CD jest opisany na okręgu o promieniu r . Wykaż, że 4r2 = |AB |⋅|CD | .

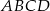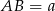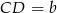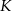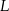Podstawy trapezu ABCD mają długości AB = a i CD = b . Na ramionach trapezu wybrano punkty K i L w ten sposób, że odcinek 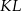KL jest równoległy do podstaw i przechodzi przez punkt przecięcia przekątnych. Oblicz długość odcinka KL .

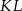Pole trapezu jest równe 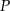P , a stosunek długości podstaw trapezu wynosi 2. Przekątne dzielą ten trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.

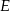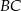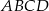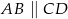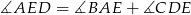Punkt E leży na ramieniu BC trapezu ABCD , w którym AB ∥ CD . Udowodnij, że ∡AED = ∡BAE + ∡CDE .

Punkt 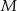M jest punktem wspólnym przekątnych trapezu prostokątnego 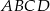ABCD . Punkt 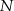N jest punktem wspólnym przekątnej 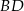BD i wysokości 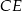CE opuszczonej na dłuższą podstawę AB . Wykaż, że |DM |2 = |MN |⋅|MB | .

PIC

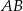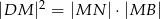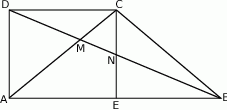
Wykaż, że punkt przecięcia przekątnych trapezu leży na prostej przechodzącej przez środki jego podstaw.

Strona 2 z 2