Na boku 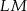 trójkąta równobocznego
trójkąta równobocznego 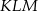 obrano taki punkt
obrano taki punkt 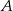 , że
, że 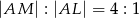 .
.
- Oblicz stosunek pól trójkątów
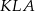 i
i 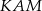 .
. - Oblicz stosunek promieni okręgów opisanych na tych trójkątach.
- Wyznacz
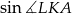 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na boku 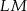 trójkąta równobocznego
trójkąta równobocznego 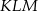 obrano taki punkt
obrano taki punkt 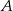 , że
, że 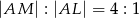 .
.
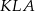 i
i 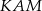 .
. 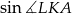 .
.Trójkąty 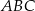 i
i 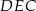 są przystającymi trójkątami równobocznymi o boku długości 6. Odcinki
są przystającymi trójkątami równobocznymi o boku długości 6. Odcinki 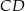 i
i 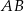 są prostopadłe, a odcinek
są prostopadłe, a odcinek 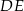 przecina odcinki
przecina odcinki 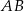 i
i 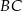 w punktach
w punktach 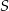 i
i 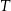 odpowiednio (zobacz rysunek). Oblicz długość odcinka
odpowiednio (zobacz rysunek). Oblicz długość odcinka 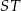 .
.
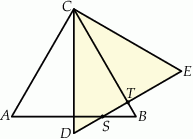
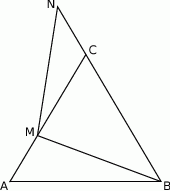
Trójkąt 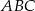 przedstawiony na poniższym rysunku jest równoboczny, a punkty
przedstawiony na poniższym rysunku jest równoboczny, a punkty 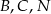 są współliniowe. Na boku
są współliniowe. Na boku 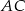 wybrano punkt
wybrano punkt 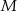 tak, że
tak, że 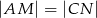 . Wykaż, że
. Wykaż, że 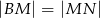 .
.
Dany jest trójkąt równoboczny 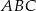 . Okrąg o średnicy
. Okrąg o średnicy 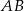 przecina bok
przecina bok 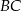 w punkcie
w punkcie 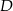 .
.
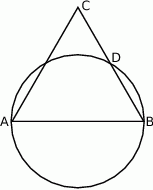
Wykaż, że 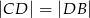 .
.
Dany jest trójkąt równoboczny 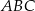 o boku długości 24. Punkt
o boku długości 24. Punkt 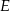 leży na boku
leży na boku 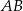 , a punkt
, a punkt 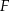 – na boku
– na boku 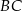 tego trójkąta. Odcinek
tego trójkąta. Odcinek 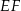 jest równoległy do boku
jest równoległy do boku 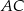 i przechodzi przez środek
i przechodzi przez środek 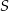 wysokości
wysokości 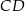 trójkąta
trójkąta 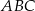 (zobacz rysunek).
(zobacz rysunek).
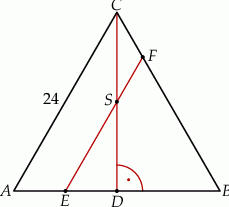
Oblicz długość odcinka 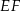 .
.
