Na bokach 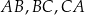 trójkąta równobocznego
trójkąta równobocznego 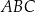 wybrano kolejno punkty
wybrano kolejno punkty 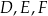 tak, że
tak, że 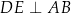 ,
, 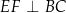 i
i 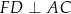 .
.

Wykaż, że trójkąt 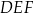 jest trójkątem równobocznym o polu trzy razy mniejszym od pola trójkąta
jest trójkątem równobocznym o polu trzy razy mniejszym od pola trójkąta 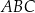 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na bokach 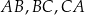 trójkąta równobocznego
trójkąta równobocznego 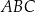 wybrano kolejno punkty
wybrano kolejno punkty 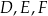 tak, że
tak, że 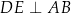 ,
, 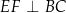 i
i 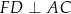 .
.

Wykaż, że trójkąt 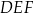 jest trójkątem równobocznym o polu trzy razy mniejszym od pola trójkąta
jest trójkątem równobocznym o polu trzy razy mniejszym od pola trójkąta 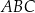 .
.
Dany jest trójkąt równoboczny 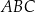 , w którym
, w którym 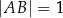 . Na boku
. Na boku 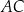 tego trójkąta wybrano taki punkt
tego trójkąta wybrano taki punkt 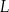 , że
, że 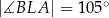 . Odcinek
. Odcinek 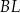 przecina wysokość
przecina wysokość 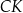 trójkąta
trójkąta 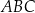 w punkcie
w punkcie 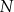 (zobacz rysunek).
(zobacz rysunek).
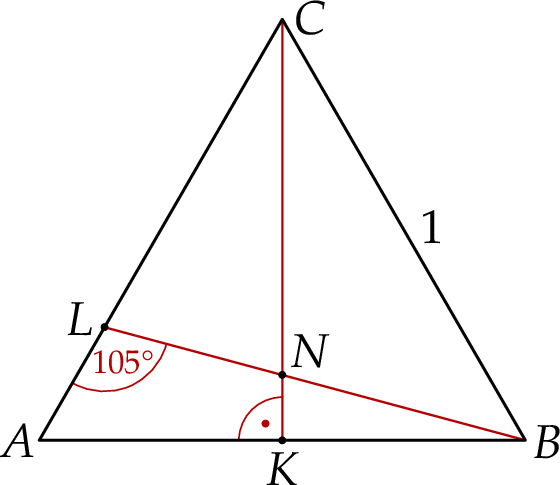
Oblicz długość odcinka 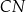 .
.
W trójkącie równobocznym 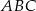 połączono środki wysokości otrzymując trójkąt
połączono środki wysokości otrzymując trójkąt 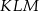 . Oblicz stosunek pól trójkątów
. Oblicz stosunek pól trójkątów 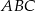 i
i 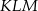 .
.
Wysokość trójkąta równobocznego jest o 3 cm krótsza od długości jego boku. Oblicz promień okręgu opisanego na tym trójkącie.
W trójkącie równobocznym 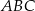 obrano na boku
obrano na boku 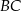 taki punkt
taki punkt 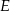 , że
, że 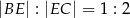 . Oblicz tangens kąta
. Oblicz tangens kąta 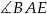 .
.
Na boku 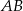 trójkąta równobocznego
trójkąta równobocznego 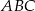 wybrano punkt
wybrano punkt 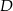 taki, że
taki, że 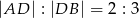 . Oblicz tangens kąta
. Oblicz tangens kąta 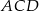 .
.
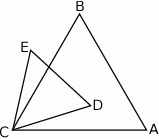
Dany jest trójkąt równoboczny 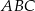 . Na bokach
. Na bokach 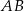 i
i 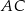 wybrano punkty – odpowiednio –
wybrano punkty – odpowiednio – 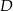 i
i 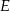 takie, że
takie, że 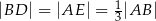 . Odcinki
. Odcinki 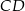 i
i 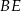 przecinają się w punkcie
przecinają się w punkcie 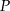 (zobacz rysunek).
(zobacz rysunek).
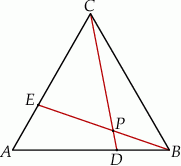
Wykaż, że pole trójkąta 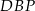 jest 21 razy mniejsze od pola trójkąta
jest 21 razy mniejsze od pola trójkąta 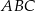 .
.
Dany jest trójkąt równoboczny 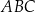 . Na bokach
. Na bokach 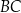 i
i 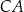 wybrano punkty – odpowiednio –
wybrano punkty – odpowiednio – 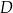 i
i 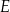 takie, że
takie, że 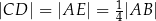 . Odcinki
. Odcinki 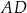 i
i 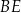 przecinają się w punkcie
przecinają się w punkcie 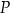 (zobacz rysunek).
(zobacz rysunek).
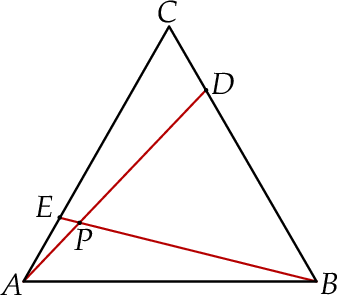
Wykaż, że pole trójkąta 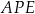 jest 52 razy mniejsze od pola trójkąta
jest 52 razy mniejsze od pola trójkąta 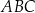 .
.
Trójkąty 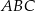 i
i 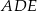 są równoboczne (zobacz rysunek). Punkty
są równoboczne (zobacz rysunek). Punkty 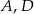 i
i 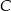 leżą na jednej prostej. Punkty
leżą na jednej prostej. Punkty 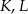 i
i 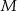 są środkami odcinków
są środkami odcinków 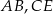 i
i 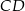 . Wykaż, że
. Wykaż, że 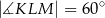 .
.
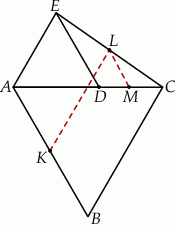
Oto w jaki sposób można uzasadnić, że suma odległości dowolnego punktu 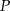 wewnątrz trójkąta równobocznego od boków tego trójkąta jest stała, tzn. nie zależy od wyboru tego punktu.
wewnątrz trójkąta równobocznego od boków tego trójkąta jest stała, tzn. nie zależy od wyboru tego punktu.
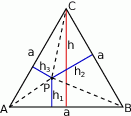
 z wierzchołkami trójkąta i zapisujemy równość pól
z wierzchołkami trójkąta i zapisujemy równość pól 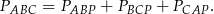
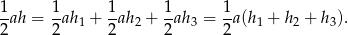
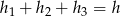 , a więc suma ta nie zależy od wyboru punktu
, a więc suma ta nie zależy od wyboru punktu 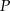 .
.Postępując w analogiczny sposób wykaż, że suma odległości dowolnego punktu 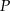 wewnątrz czworościanu foremnego od jego ścian jest stała, to znaczy nie zależy od wyboru punktu
wewnątrz czworościanu foremnego od jego ścian jest stała, to znaczy nie zależy od wyboru punktu 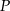 .
.
Ze środka ciężkości trójkąta równobocznego o boku  , wykreślono okrąg o promieniu
, wykreślono okrąg o promieniu 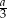 . Oblicz pole części koła nie należącego do trójkąta.
. Oblicz pole części koła nie należącego do trójkąta.
Na trójkącie równobocznym opisano drugi trójkąt równoboczny tak, że wierzchołki pierwszego trójkąta leżą na bokach drugiego. Boki obydwu trójkątów tworzą kąty 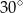 . Jakim procentem pola małego trójkąta jest pole dużego trójkąta?
. Jakim procentem pola małego trójkąta jest pole dużego trójkąta?
Oblicz długość boku kwadratu wpisanego w trójkąt równoboczny o boku  .
.
Okrąg wpisany w trójkąt równoboczny 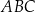 jest jednocześnie okręgiem opisanym na trójkącie równobocznym
jest jednocześnie okręgiem opisanym na trójkącie równobocznym 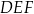 . O ile procent pole trójkąta
. O ile procent pole trójkąta 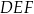 jest mniejsze od pola trójkąta
jest mniejsze od pola trójkąta 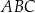 ?
?
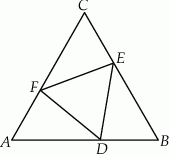
W trójkąt równoboczny 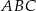 wpisano trójkąt
wpisano trójkąt 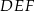 (patrz rysunek), tak że
(patrz rysunek), tak że 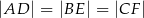 . Udowodnij, że trójkąt
. Udowodnij, że trójkąt 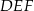 jest równoboczny.
jest równoboczny.
Na boku 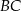 trójkąta równobocznego
trójkąta równobocznego 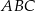 wybrano taki punkt
wybrano taki punkt 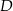 , że pole trójkąta
, że pole trójkąta 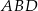 jest równe
jest równe 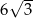 i jest dwa razy większe od pola trójkąta
i jest dwa razy większe od pola trójkąta 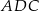 (zobacz rysunek).
(zobacz rysunek).
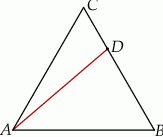
Oblicz długość odcinka 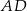 .
.
Trójkąty 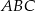 i
i 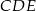 są równoboczne. Punkty
są równoboczne. Punkty 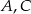 i
i 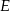 leżą na jednej prostej. Punkty
leżą na jednej prostej. Punkty 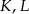 i
i 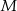 są środkami odcinków
są środkami odcinków 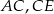 i
i 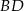 (zobacz rysunek). Wykaż, że punkty
(zobacz rysunek). Wykaż, że punkty 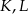 i
i 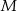 są wierzchołkami trójkąta równobocznego.
są wierzchołkami trójkąta równobocznego.
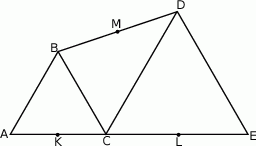
Trójkąty 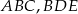 i
i 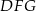 są równoboczne oraz
są równoboczne oraz 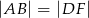 . Punkty
. Punkty 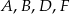 leżą na jednej prostej. Punkty
leżą na jednej prostej. Punkty 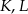 i
i 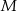 są środkami odcinków
są środkami odcinków 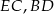 i
i 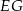 . Wykaż, że punkty
. Wykaż, że punkty 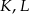 i
i 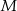 są wierzchołkami trójkąta równobocznego.
są wierzchołkami trójkąta równobocznego.
Niech 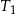 będzie trójkątem równobocznym o boku długości
będzie trójkątem równobocznym o boku długości  . Konstruujemy kolejno trójkąty równoboczne
. Konstruujemy kolejno trójkąty równoboczne 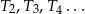 takie, że bok kolejnego trójkąta jest równy wysokości poprzedniego trójkąta. Oblicz sumę pól trójkątów
takie, że bok kolejnego trójkąta jest równy wysokości poprzedniego trójkąta. Oblicz sumę pól trójkątów 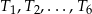 .
.
Dany jest trójkąt równoboczny 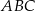 o boku długości 16. Na boku
o boku długości 16. Na boku 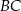 obrano punkt
obrano punkt 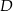 dzielący ten bok w stosunku 3:5, licząc od punktu
dzielący ten bok w stosunku 3:5, licząc od punktu 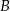 . Oblicz sinus kąta
. Oblicz sinus kąta 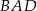 .
.
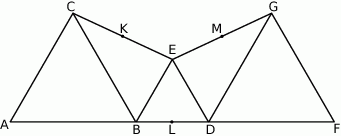
Trójkąty równoboczne 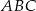 i
i 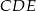 są położone tak, jak na poniższym rysunku. Wykaż, że
są położone tak, jak na poniższym rysunku. Wykaż, że 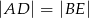 .
.
Trójkąt równoboczny 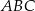 ma pole równe
ma pole równe 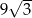 . Prosta równoległa do boku
. Prosta równoległa do boku 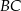 przecina boki
przecina boki 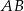 i
i 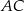 – odpowiednio – w punktach
– odpowiednio – w punktach 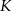 i
i 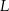 . Trójkąty
. Trójkąty 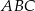 i
i 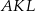 są podobne, a stosunek długości boków tych trójkątów jest równy
są podobne, a stosunek długości boków tych trójkątów jest równy  . Oblicz długość boku trójkąta
. Oblicz długość boku trójkąta 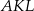 .
.
Trójkąt równoboczny 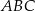 ma pole równe
ma pole równe 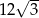 . Prosta równoległa do boku
. Prosta równoległa do boku 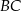 przecina boki
przecina boki 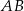 i
i 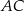 – odpowiednio – w punktach
– odpowiednio – w punktach 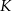 i
i 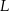 . Stosunek obwodów trójkątów
. Stosunek obwodów trójkątów 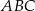 i
i 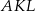 jest równy
jest równy 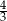 . Oblicz długość boku trójkąta
. Oblicz długość boku trójkąta 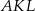 .
.
Z punktu 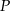 należącego do boku
należącego do boku 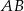 trójkąta równobocznego
trójkąta równobocznego 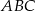 poprowadzono półprostą dzielącą trójkąt na dwie figury o równych polach. Oblicz tangens kąta jaki tworzy ta półprosta z odcinkiem
poprowadzono półprostą dzielącą trójkąt na dwie figury o równych polach. Oblicz tangens kąta jaki tworzy ta półprosta z odcinkiem 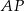 , jeśli
, jeśli 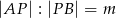 i
i 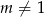 .
.
