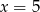Zadanie nr 9847239
Liczby 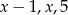 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Rozwiązanie
Oczywiście 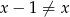 , więc musimy mieć
, więc musimy mieć 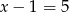 lub
lub 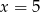 . Daje nam to trójkąty o bokach 5,6,5 lub 4,5,5.
. Daje nam to trójkąty o bokach 5,6,5 lub 4,5,5.
Odpowiedź: 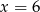 lub
lub 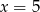
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Liczby 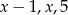 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Oczywiście 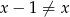 , więc musimy mieć
, więc musimy mieć 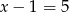 lub
lub 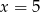 . Daje nam to trójkąty o bokach 5,6,5 lub 4,5,5.
. Daje nam to trójkąty o bokach 5,6,5 lub 4,5,5.
Odpowiedź: 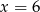 lub
lub