Zadanie nr 3321451
Dany jest trójkąt równoramienny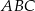 
, w którym 
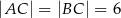, a punkt 
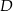jest środkiem podstawy 
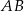. Okrąg o środku 
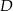jest styczny do prostej 
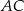w punkcie 
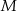. Punkt 
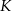leży na boku 
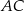, punkt 
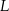leży na boku 
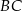, odcinek 
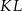jest styczny do rozważanego okręgu oraz 
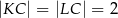(zobacz rysunek).
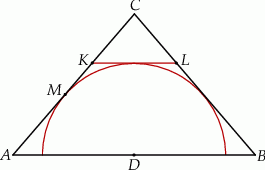
Wykaż, że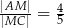 
.
Rozwiązanie
Prosta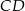 
jest osią symetrii danego rysunku, więc przecina odcinek 
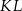w jego środku – oznaczmy ten punkt przez 
.
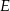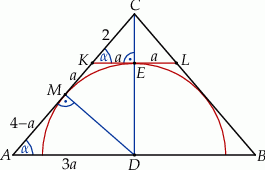
Jeżeli oznaczymy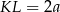 
, to 
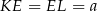oraz
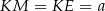
(odcinki stycznych do okręgów). Wiemy ponadto, że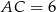 
, więc
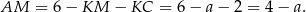
Wiemy też, że trójkąty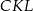 
i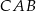 
są podobne w skali 
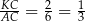. Zatem 
.
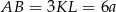W tym miejscu kończą się łatwe obserwacje – jeżeli mamy pójść dalej musimy jakoś wykorzystać fakt, że środkiem narysowanego okręgu jest środek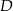 
boku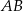 
– na razie tej informacji nie wykorzystaliśmy. W tym celu dorysowujemy promień 
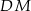, który jest oczywiście prostopadły do stycznej w punkcie 
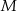, czyli do prostej 
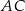. Jeżeli to zrobimy i chwilę popatrzymy na otrzymaną konfigurację, to można zauważyć, że otrzymaliśmy dwa podobne trójkąty prostokątne – 
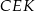i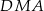 
. To podobieństwo pozwala obliczyć 
.
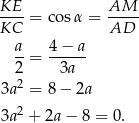
Rozwiązujemy otrzymane równanie kwadratowe.
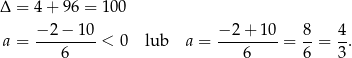
To oznacza, że
