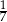Zadanie nr 5918856
W trójkącie równoramiennym 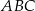 :
: 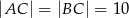 , a miara kąta
, a miara kąta 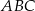 jest równa
jest równa 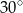 . Na boku
. Na boku 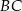 wybrano punkt
wybrano punkt 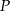 , taki, że
, taki, że 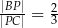 . Oblicz sinus kąta
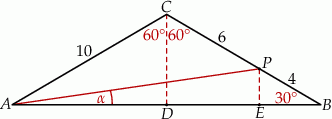
. Oblicz sinus kąta  (zobacz rysunek).
(zobacz rysunek).
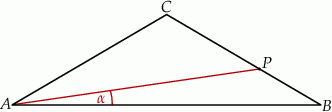
Rozwiązanie
Niech 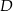 i
i 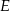 będą rzutami punktów
będą rzutami punktów 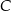 i
i 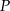 na bok
na bok 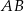
Sposób I
Szukany 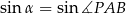 obliczymy z twierdzenia sinusów w trójkącie
obliczymy z twierdzenia sinusów w trójkącie 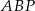 , ale zanim to zrobimy obliczamy długość odcinka
, ale zanim to zrobimy obliczamy długość odcinka 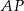 . Stosujemy twierdzenie cosinusów w trójkącie
. Stosujemy twierdzenie cosinusów w trójkącie 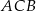 .
.
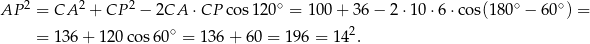
Zatem 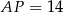 i na mocy twierdzenia sinusów w trójkącie
i na mocy twierdzenia sinusów w trójkącie 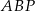 mamy
mamy
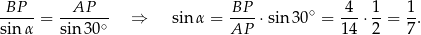
Sposób II
Tym razem obejdziemy się bez twierdzenia sinusów. Jeżeli 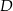 i
i 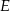 są rzutami odpowiednio punktów
są rzutami odpowiednio punktów 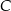 i
i 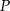 na postawę
na postawę 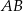 , to każdy z trójkątów
, to każdy z trójkątów 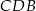 i
i 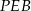 jest połówką trójkąta równobocznego, więc
jest połówką trójkąta równobocznego, więc
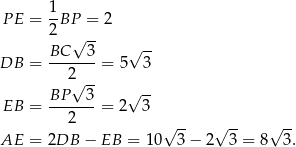
Stosujemy teraz twierdzenie Pitagorasa w trójkącie 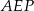 .
.
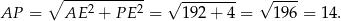
Mamy zatem
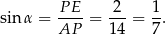
Sposób III
Trójkąt 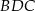 jest prostokątny, więc
jest prostokątny, więc
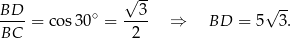
Piszemy teraz twierdzenie sinusów w trójkącie 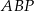 .
.
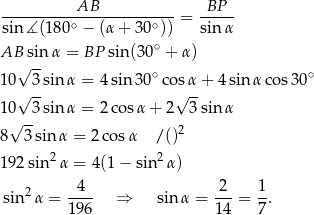
Odpowiedź: