Wyznacz ekstrema lokalne funkcji 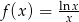 .
.
/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne/Ekstrema
Wyznacz ekstrema funkcji 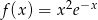 .
.
Wyznacz wartość największą i najmniejszą funkcji 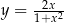 w przedziale
w przedziale 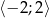 .
.
Dana jest funkcja 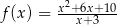 .
.
- Określ przedziały monotoniczności tej funkcji.
- Znajdź ekstrema lokalne funkcji
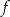 .
.
Wyznacz najmniejszą 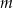 i największą
i największą 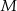 wartość funkcji
wartość funkcji 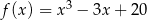 w przedziale
w przedziale 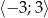 .
.
Wyznacz ekstrema funkcji 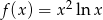 .
.
Wyznacz wszystkie argumenty  , w których funkcja
, w których funkcja 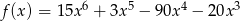 ma ekstrema lokalne.
ma ekstrema lokalne.
Wyznacz wartość największą i najmniejszą funkcji 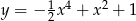 w przedziale
w przedziale 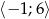 .
.
Wykaż, że funkcja 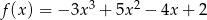 nie ma ekstremum.
nie ma ekstremum.
Wyznacz te argumenty, dla których funkcja 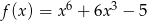 osiąga wartość najmniejszą.
osiąga wartość najmniejszą.
Wyznacz przedziały monotoniczności i ekstrema lokalne funkcji 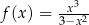 .
.
Wyznacz ekstrema lokalne funkcji 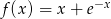 .
.
Wyznacz ekstrema lokalne funkcji 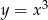 .
.
Ukryj
Podobne zadania
Wyznacz ekstrema lokalne funkcji 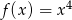 .
.
Wyznacz ekstrema lokalne funkcji 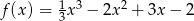 .
.
Dana jest funkcja 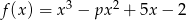 .
.
- Znajdź taką wartość
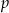 , dla której funkcja
, dla której funkcja 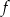 osiąga minimum w punkcie
osiąga minimum w punkcie 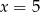 .
. - Dla wyznaczonego
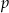 podaj przedziały monotoniczności funkcji
podaj przedziały monotoniczności funkcji 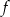 .
.

