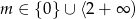Zadanie nr 4000672
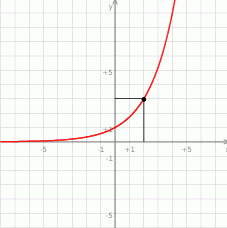
Na rysunku przedstawiony jest wykres funkcji wykładniczej 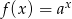 dla
dla 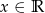 .
.
- Oblicz
 .
. - Narysuj wykres funkcji
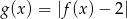 i podaj wszystkie wartości parametru
i podaj wszystkie wartości parametru 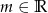 , dla których równanie
, dla których równanie 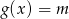 ma dokładnie jedno rozwiązanie.
ma dokładnie jedno rozwiązanie.
Rozwiązanie
- Z obrazka widzimy, że wykres przechodzi przez punkt
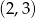 , czyli
, czyli 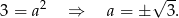
Ponieważ mamy do czynienia z funkcją wykładniczą musi być
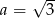 .
.
Odpowiedź: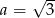
- Wykres funkcji
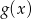 powstaje przez przesunięcie wykresu funkcji
powstaje przez przesunięcie wykresu funkcji 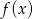 o 2 jednostki w dół, a potem odbicie części pod osią
o 2 jednostki w dół, a potem odbicie części pod osią 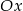 do góry.
do góry. 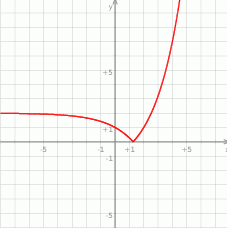
Z wykresu odczytujemy, że równanie
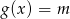 ma dokładnie jedno rozwiązanie dla
ma dokładnie jedno rozwiązanie dla 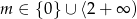 .
.
Odpowiedź: