/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna/Z wymierną

Zadanie nr 6418530

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest funkcja 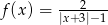---2--- f(x ) = |x+3|− 1 .

  • Naszkicuj wykres funkcji 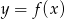y = f (x) i na jego podstawie wyznacz liczbę rozwiązań równania 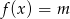f (x) = m w zależności od parametru m .
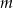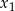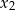  • Liczby x1 i x2 są różnymi pierwiastkami równania 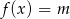f (x) = m . Oblicz x1 + x2 .

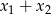Rozwiązanie

  • Zauważmy, że
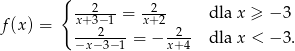
    { --2---= -2-- dla x ≥ − 3 f (x) = x+-3−21-- x+2-2-- −x−3− 1 = − x+4 dla x < − 3.

    Zatem na prawo od -3 mamy hiperbolę 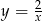y = 2 x przesuniętą o 2 jednostki w lewo, a na lewo od -3 hiperbolę 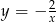2 y = − x przesuniętą 4 jednostki w lewo. Teraz wykonujemy szkicowy rysunek.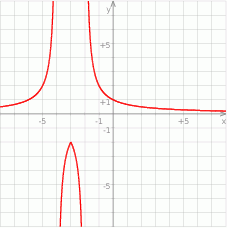

    PIC

    Z wykresu odczytujemy liczbę rozwiązań równania f(x) = m .

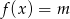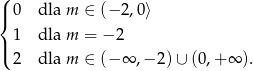
    ( |{ 0 dla m ∈ (− 2,0⟩ 1 dla m = − 2 |( 2 dla m ∈ (− ∞ ,− 2) ∪ (0,+ ∞ ).

     
    Odpowiedź: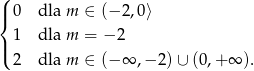 ( | 0 dla m ∈ (− 2,0⟩ { | 1 dla m = − 2 ( 2 dla m ∈ (− ∞ ,− 2)∪ (0 ,+∞ ).

  •  

    Sposób I

    Przekształćmy interesujące nas równanie

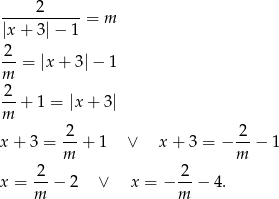
    ----2------= m |x + 3 |− 1 2 --= |x+ 3|− 1 m 2-+ 1 = |x+ 3| m 2- 2- x + 3 = m + 1 ∨ x + 3 = − m − 1 2 2 x = -- − 2 ∨ x = − --− 4. m m

    Zatem suma pierwiastków jest równa

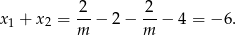
    x + x = 2-− 2− 2-− 4 = − 6. 1 2 m m

    Sposób II

    Zauważmy, że wykres funkcji 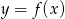y = f(x ) powstaje z wykresu funkcji 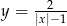--2-- y = |x|− 1 przez przesunięcie o 3 jednostki w lewo. Funkcja 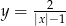--2-- y = |x|− 1 jest funkcją parzystą, więc ma oś symetrii 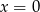x = 0 . To oznacza, że wykres funkcji 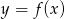y = f(x) również ma oś symetrii – prostą 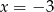x = − 3 . Ponadto, z poprzedniego podpunktu wiemy, że jeżeli równanie 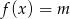f (x ) = m ma co najmniej dwa pierwiastki, to ma dokładnie dwa pierwiastki. 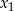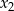W połączeniu z symetrią wykresu oznacza to, że liczby x 1 i x2 leżą symetrycznie względem prostej 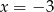x = − 3 . Zatem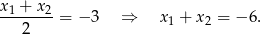

    x1 + x2 ---2----= − 3 ⇒ x1 + x2 = − 6.

    Sposób III

    Przekształćmy interesujące nas równanie

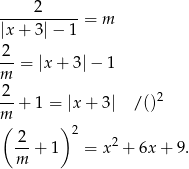
    ----2------= m |x + 3 |− 1 2 --= |x+ 3|− 1 m 2-+ 1 = |x+ 3| /()2 m ( 2 ) 2 --+ 1 = x2 + 6x + 9. m

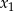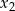    Zatem liczby x1 i x 2 są pierwiastkami powyższego równania kwadratowego. Na mocy wzorów Viète’a mamy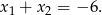

    x1 + x2 = − 6.

     
    Odpowiedź: x1 + x2 = − 6

Wersja PDF
Rozwiązanie Losuj ponownie