/Szkoła średnia/Prawdopodobieństwo/Z definicji/Różne

Zadanie nr 3484128

Rzucamy sześcienną kostką i monetą. Jakie jest prawdopodobieństwo, że na monecie wypadnie reszka, a na kostce nie więcej niż 4 oczka.

Rozwiązanie

Sposób I

Prawdopodobieństwo tego, że wypadnie reszka jest równe 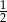1 2 , a prawdopodobieństwo, że wypadną nie więcej niż 4 oczka jest równe 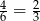46 = 23 . Zdarzenia są od siebie niezależne (wynik jednego nie ma wpływu na wynik drugiego), więc

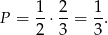
1- 2- 1- P = 2 ⋅ 3 = 3 .

Sposób II

Jeżeli za zdarzenia sprzyjające przyjmiemy pary: wynik rzutu kostką i monetą, to mamy

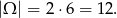
|Ω | = 2 ⋅6 = 12 .

Zdarzenia sprzyjające to

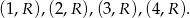
(1,R ),(2 ,R),(3,R ),(4,R).

Zatem prawdopodobieństwo wynosi

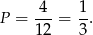
4 1 P = 1-2 = 3-.

Odpowiedź: 1 3

Wersja PDF