Długości boków trójkąta tworzą trzy kolejne wyrazy ciągu arytmetycznego o różnicy 1. Oblicz długości boków tego trójkąta, jeśli jego pole wynosi 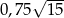 .
.
/Szkoła średnia/Ciągi/Arytmetyczny
O liczbach 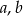 i
i  wiadomo, że tworzą ciąg arytmetyczny oraz ich suma wynosi
wiadomo, że tworzą ciąg arytmetyczny oraz ich suma wynosi 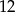 . Wyznacz największą możliwą wartość wyrażenia
. Wyznacz największą możliwą wartość wyrażenia 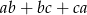 . Dla jakich liczb
. Dla jakich liczb 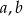 i
i  wartość ta jest osiągana.
wartość ta jest osiągana.
Wykaż, że dla każdego 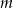 ciąg
ciąg 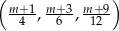 jest arytmetyczny.
jest arytmetyczny.
Wykaż, że dla każdego 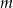 ciąg
ciąg 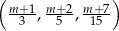 jest arytmetyczny.
jest arytmetyczny.
Długości boków trójkąta są kolejnymi wyrazami ciągu arytmetycznego. Obwód trójkąta jest równy 33, a cosinus największego kąta jest równy  . Oblicz promień okręgu opisanego na tym trójkącie.
. Oblicz promień okręgu opisanego na tym trójkącie.
Sprawdź, czy liczby 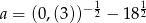 ,
, 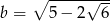 ,
, 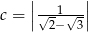 są w podanej kolejności kolejnymi wyrazami ciągu arytmetycznego.
są w podanej kolejności kolejnymi wyrazami ciągu arytmetycznego.
Jedno z rozwiązań równania 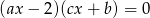 jest równe 6. Ciąg
jest równe 6. Ciąg 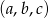 jest ciągiem arytmetycznym, w którym pierwszy wyraz jest o 8 większy od trzeciego. Znajdź drugie rozwiązanie tego równania.
jest ciągiem arytmetycznym, w którym pierwszy wyraz jest o 8 większy od trzeciego. Znajdź drugie rozwiązanie tego równania.
Czwarty wyraz ciągu arytmetycznego jest równy 6. Oblicz sumę siedmiu początkowych wyrazów tego ciągu.
W malejącym ciągu arytmetycznym 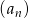 spełnione są warunki
spełnione są warunki 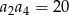 oraz
oraz 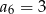 . Wyznacz sumę 10 początkowych wyrazów tego ciągu.
. Wyznacz sumę 10 początkowych wyrazów tego ciągu.

