/Szkoła średnia/Ciągi/Arytmetyczny

Zadanie nr 2487651

Długości boków prostokąta i długość jego przekątnej tworzą ciąg arytmetyczny. Oblicz długości jego boków, jeśli obwód prostokąta jest równy 14.

Wersja PDF

Rozwiązanie

Przekątna prostokąta jest zawsze dłuższa od każdego z boków, wiec jest to największy wyraz ciągu.

PIC

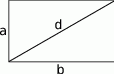
Oznaczmy jej długość przez 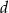d , a długości boków przez 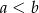a < b . Mamy wtedy warunki

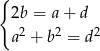
{ 2b = a + d 2 2 2 a + b = d

Wstawmy 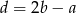d = 2b − a do drugiego równania

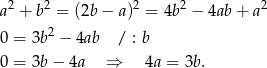
2 2 2 2 2 a + b = (2b− a) = 4b − 4ab + a 0 = 3b2 − 4ab / : b 0 = 3b − 4a ⇒ 4a = 3b.

Wiemy dodatkowo, że 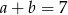a + b = 7 . Podstawmy 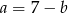a = 7− b we wcześniej otrzymanej równości

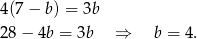
4 (7− b) = 3b 2 8− 4b = 3b ⇒ b = 4.

Daje to nam 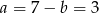a = 7− b = 3 .  
Odpowiedź: 3 i 4

Wersja PDF