Zadanie nr 9062712
Suma ośmiu początkowych wyrazów ciągu arytmetycznego 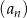 , określonego dla
, określonego dla 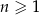 , jest równa 90, a suma
, jest równa 90, a suma 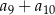 jest równa 57,5. Oblicz pierwszy wyraz i różnicę tego ciągu.
jest równa 57,5. Oblicz pierwszy wyraz i różnicę tego ciągu.
Rozwiązanie
Sposób I
Korzystamy ze wzorów na 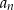 i
i 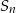 .
.
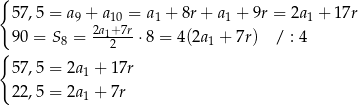
Odejmując od pierwszego równania drugie (żeby skrócić 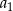 ) mamy
) mamy
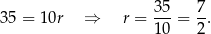
Z drugiego równania mamy
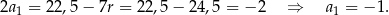
Sposób II
Na mocy wzoru 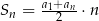 na sumę
na sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 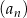 , mamy
, mamy
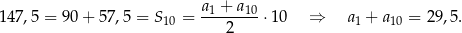
Stąd
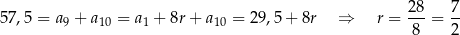
oraz
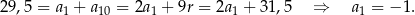
Odpowiedź: