Zadanie nr 8459063
Dany jest okrąg 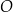 . Przez punkt
. Przez punkt 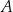 poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio –
poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio – 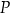 oraz
oraz 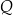 . Przez punkt
. Przez punkt 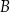 leżący na odcinku
leżący na odcinku 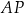 poprowadzono styczną do tego okręgu w punkcie
poprowadzono styczną do tego okręgu w punkcie 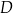 , która przecięła odcinek
, która przecięła odcinek  w punkcie
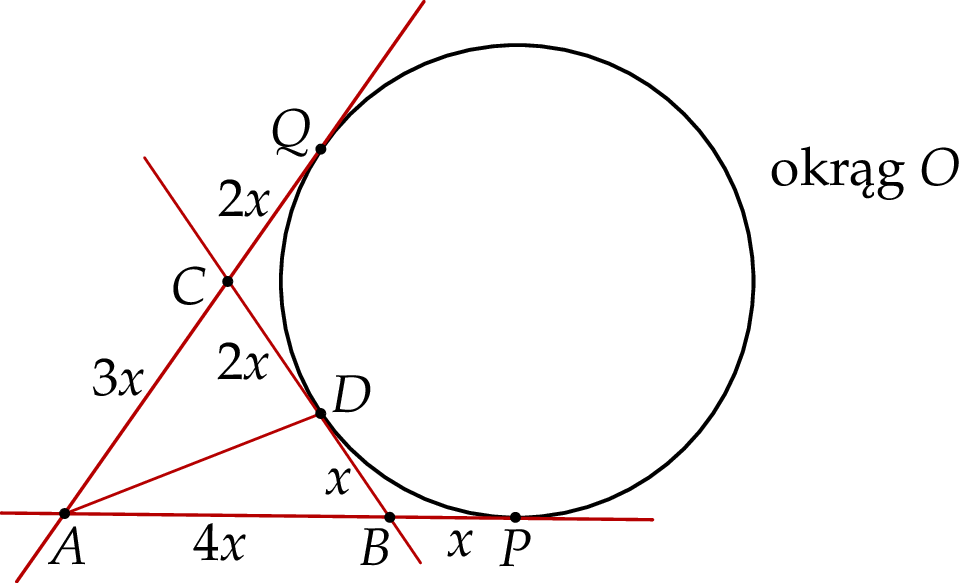
w punkcie 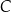 (zobacz rysunek).
(zobacz rysunek).
Wykaż, że jeżeli 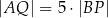 oraz
oraz 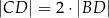 , to trójkąt
, to trójkąt 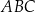 jest równoramienny.
jest równoramienny.
Rozwiązanie
W rozwiązaniu kilkukrotnie skorzystamy z tego, że odcinki stycznych do okręgu poprowadzonych z jednego punktu mają równą długość. Taką sytuację mamy np. na danym rysunku w przypadku odcinków 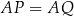 ,
, 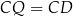 i
i 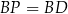 . Żeby się nie pogubić oznaczmy
. Żeby się nie pogubić oznaczmy
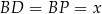
i przy pomocy tego odcinka spróbujemy obliczyć długości wszystkich pozostałych odcinków na rysunku.
Z treści zadania wiemy, że
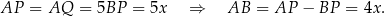
Ponadto,
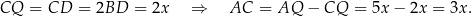
Udało nam się w tym momencie obliczyć długości wszystkich boków trójkąta 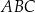 i faktycznie jest on równoramienny
i faktycznie jest on równoramienny