Zadanie nr 9574876
Na bokach 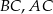 i
i 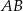 trójkąta
trójkąta 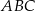 wybrano odpowiednio punkty
wybrano odpowiednio punkty 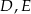 i
i 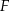 . Wykaż, że jeżeli okręgi opisane na trójkątach
. Wykaż, że jeżeli okręgi opisane na trójkątach 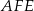 i
i 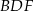 są styczne, to punkt
są styczne, to punkt 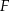 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 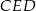 .
.
Rozwiązanie
Jednym z najtrudniejszych elementów tego zadania to wykonanie prawidłowego rysunku – najlepiej jest najpierw narysować okręgi styczne, a potem dorysować do niech trójkąt 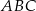 .
.
Musimy udowodnić, że na czworokącie 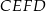 można opisać okrąg.
można opisać okrąg.
Sposób I
Wystarczy wykazać, że
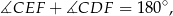
a ten warunek jest równoważny warunkowi
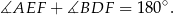
Oznaczmy 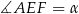 i
i 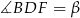 . Patrzymy najpierw na trójkąt równoramienny
. Patrzymy najpierw na trójkąt równoramienny 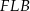 . Mamy w nim
. Mamy w nim
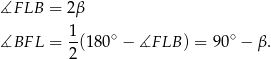
Podobnie obliczamy kąty trójkąta równoramiennego 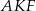 . Kąt wklęsły przy wierzchołku
. Kąt wklęsły przy wierzchołku 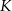 tego trójkąta jest równy
tego trójkąta jest równy 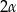 (bo jest oparty na tym samym łuku, co kąt
(bo jest oparty na tym samym łuku, co kąt 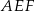 ), więc kąt wypukły przy wierzchołku
), więc kąt wypukły przy wierzchołku 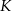 jest równy
jest równy 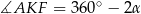 . Mamy stąd
. Mamy stąd
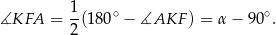
Teraz wystarczy zauważyć, że 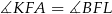 , więc
, więc
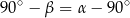
Zatem rzeczywiście 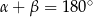 .
.
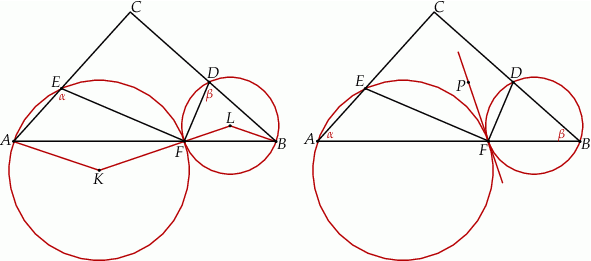
Sposób II
Tym razem oznaczmy 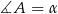 i
i 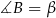 oraz dorysujmy wspólną styczną do danych okręgów. Niech jeszcze
oraz dorysujmy wspólną styczną do danych okręgów. Niech jeszcze 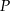 będzie jakimkolwiek punktem tej stycznej, który leży wewnątrz czworokąta
będzie jakimkolwiek punktem tej stycznej, który leży wewnątrz czworokąta 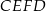 . Na mocy twierdzenia o stycznej mamy
. Na mocy twierdzenia o stycznej mamy
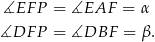
Stąd
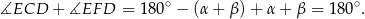
To oznacza, że rzeczywiście na czworokącie 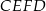 można opisać okrąg.
można opisać okrąg.

