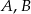 są zdarzeniami losowymi zawartymi w
są zdarzeniami losowymi zawartymi w 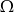 . Wykaż, że jeżeli
. Wykaż, że jeżeli 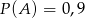 i
i 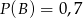 , to
, to 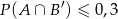 (
(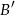 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 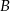 ).
).
/Szkoła średnia/Prawdopodobieństwo/Bez treści
Wiadomo, że 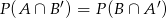 ,
, 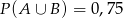 ,
, 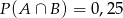 . Oblicz:
. Oblicz: 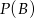 i
i 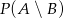 .
.
O zdarzeniach losowych 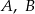 wiadomo, że:
wiadomo, że: 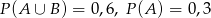 i
i 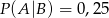 . Oblicz prawdopodobieństwo warunkowe
. Oblicz prawdopodobieństwo warunkowe 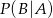 .
.
O zdarzeniach losowych 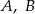 wiadomo, że:
wiadomo, że: 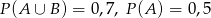 i
i 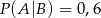 . Oblicz prawdopodobieństwo warunkowe
. Oblicz prawdopodobieństwo warunkowe 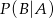 .
.
Zdarzenia losowe 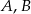 są zawarte w
są zawarte w 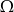 oraz
oraz 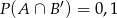 i
i 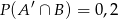 . Wykaż, że
. Wykaż, że 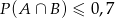 (
(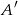 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 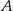 ,
, 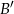 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 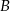 ).
).
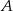 i
i 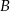 są takim zdarzeniami losowymi zawartymi w
są takim zdarzeniami losowymi zawartymi w 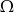 , że
, że 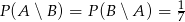 i
i 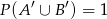 . Oblicz
. Oblicz 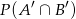 .
.
Oblicz prawdopodobieństwo 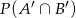 , jeśli
, jeśli 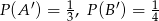 i
i 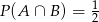 .
.
Oblicz prawdopodobieństwo 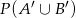 , jeśli
, jeśli 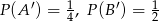 i
i 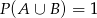 .
.
Wykaż, że jeśli 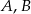 są dowolnymi zdarzeniami przestrzeni
są dowolnymi zdarzeniami przestrzeni 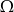 , to
, to 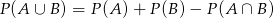 .
.
Wiadomo, że 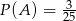 ,
, 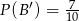 ,
, 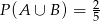 . Oblicz
. Oblicz 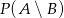 i
i 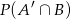 .
.
Wiadomo że 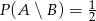 ,
, 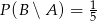 ,
, 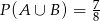 . Oblicz
. Oblicz 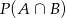 .
.
Wykaż, że jeżeli 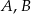 są podzbiorami
są podzbiorami 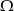 oraz
oraz 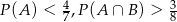 , to
, to 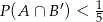 .
.
Wykaż, że jeżeli 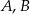 są podzbiorami
są podzbiorami 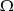 oraz
oraz 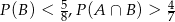 , to
, to 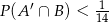 (
(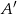 oznacza zdarzenie przeciwne do
oznacza zdarzenie przeciwne do 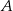 ).
).
Wykaż, że jeżeli prawdopodobieństwa zdarzeń 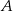 i
i 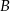 spełniają warunki:
spełniają warunki: 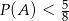 i
i 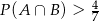 , to
, to
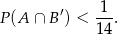
O zdarzeniach 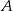 i
i 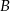 wiadomo, że
wiadomo, że 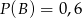 ,
, 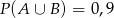 oraz
oraz 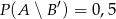 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 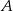 .
.
Zdarzenia losowe 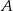 i
i 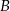 są zawarte w przestrzeni
są zawarte w przestrzeni 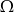 . Wiedząc, że
. Wiedząc, że 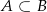 oraz
oraz 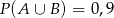 , oblicz
, oblicz 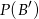 .
.
O zdarzeniach 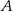 i
i 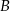 wiadomo, że
wiadomo, że 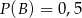 ;
; 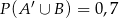 ;
; 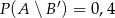 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 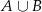 .
.
O zdarzeniach 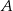 i
i 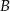 wiadomo, że
wiadomo, że 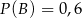 ;
; 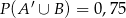 ;
; 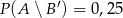 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 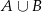 .
.
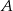 i
i 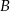 są takimi zdarzeniami losowymi zawartymi w
są takimi zdarzeniami losowymi zawartymi w 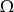 , że
, że 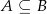 oraz
oraz 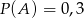 i
i 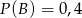 . Oblicz prawdopodobieństwo
. Oblicz prawdopodobieństwo 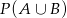 .
.

