Okrąg przecina boki czworokąta 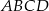 kolejno w punktach
kolejno w punktach 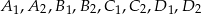 (zobacz rysunek).
(zobacz rysunek).
Wykaż, że jeżeli 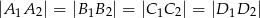 , to w czworokąt
, to w czworokąt 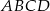 można wpisać okrąg.
można wpisać okrąg.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Okrąg przecina boki czworokąta 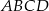 kolejno w punktach
kolejno w punktach 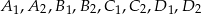 (zobacz rysunek).
(zobacz rysunek).

Wykaż, że jeżeli 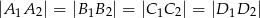 , to w czworokąt
, to w czworokąt 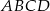 można wpisać okrąg.
można wpisać okrąg.
Dany jest czworokąt wypukły 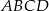 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 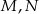 są odpowiednio środkami boków
są odpowiednio środkami boków 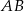 i
i 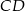 . Punkty
. Punkty 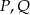 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 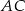 i
i 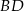 . Uzasadnij, że
. Uzasadnij, że 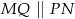 .
.
Dany jest czworokąt wypukły 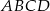 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 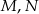 są odpowiednio środkami boków
są odpowiednio środkami boków 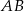 i
i 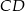 . Punkty
. Punkty 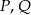 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 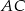 i
i 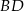 . Uzasadnij, że czworokąt
. Uzasadnij, że czworokąt 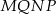 jest równoległobokiem.
jest równoległobokiem.
Wykaż, że jeżeli w czworokącie 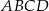 dwusieczne kątów przy wierzchołkach
dwusieczne kątów przy wierzchołkach 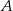 i
i 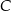 przecinają dwusieczne kątów przy wierzchołkach
przecinają dwusieczne kątów przy wierzchołkach 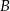 i
i 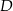 w czterech różnych punktach, to punkty te leżą na pewnym okręgu.
w czterech różnych punktach, to punkty te leżą na pewnym okręgu.
Udowodnij, że jeżeli środki boków dwóch czworokątów wypukłych pokrywają się, to pola tych czworokątów są równe.
W czworokącie 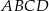 spełniony jest warunek
spełniony jest warunek 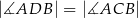 . Wykaż, że na czworokącie
. Wykaż, że na czworokącie 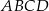 można opisać okrąg.
można opisać okrąg.
Dany jest taki czworokąt wypukły 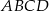 , że okręgi wpisane w trójkąty
, że okręgi wpisane w trójkąty 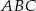 i
i 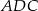 są styczne. Wykaż, że w czworokąt
są styczne. Wykaż, że w czworokąt 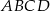 można wpisać okrąg.
można wpisać okrąg.
Udowodnij, że w czworokącie wpisanym w okrąg suma iloczynów długości przeciwległych boków jest równa iloczynowi długości przekątnych (twierdzenie Ptolemeusza).
Dany jest czworokąt wypukły 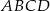 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 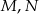 są odpowiednio środkami boków
są odpowiednio środkami boków 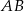 i
i 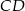 . Punkty
. Punkty 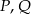 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 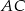 i
i 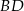 . Uzasadnij, że jeżeli odcinki
. Uzasadnij, że jeżeli odcinki 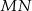 i
i 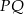 są prostopadłe, to
są prostopadłe, to 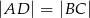 .
.
Wykaż, że jeżeli odcinki łączące środki przeciwległych boków czworokąta są prostopadłe, to przekątne tego czworokąta mają równe długości.
Uzasadnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku. Jaka figurę otrzymamy, łącząc kolejno środki boków: a) rombu, b) prostokąta, c) kwadratu?
Uzasadnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku.
Przekątne czworokąta wypukłego 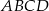 przecinają się w punkcie
przecinają się w punkcie 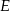 . Wiadomo, że trójkąty
. Wiadomo, że trójkąty 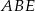 i
i 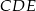 mają równe pola, długość boku
mają równe pola, długość boku 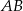 jest równa 4, a przekątna
jest równa 4, a przekątna 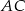 jest zawarta w dwusiecznej kąta
jest zawarta w dwusiecznej kąta 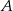 . Oblicz długość boku
. Oblicz długość boku 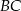 .
.
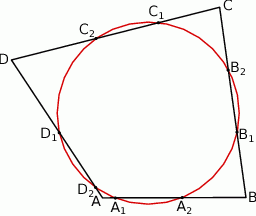
Przez każde dwa sąsiednie wierzchołki czworokąta 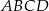 wpisanego w okrąg poprowadzono okrąg (zobacz rysunek).
wpisanego w okrąg poprowadzono okrąg (zobacz rysunek).
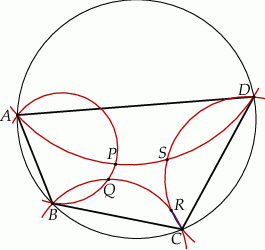
Wykaż, że punkty 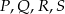 , w których przecinają się te okręgi, leżą na jednym okręgu.
, w których przecinają się te okręgi, leżą na jednym okręgu.
Przedłużenia przeciwległych boków czworokąta wpisanego w okrąg tworzą kąty ostre o miarach 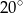 i
i 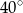 . Oblicz miary kątów czworokąta.
. Oblicz miary kątów czworokąta.
