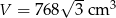Zadanie nr 6008958
Dany jest graniastosłup czworokątny prosty 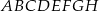 o podstawach
o podstawach 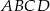 i
i 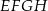 oraz krawędziach bocznych
oraz krawędziach bocznych 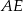 ,
, 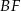 ,
, 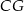 ,
, 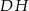 . Podstawa
. Podstawa 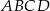 graniastosłupa jest rombem o boku długości 8 cm i kątach ostrych
graniastosłupa jest rombem o boku długości 8 cm i kątach ostrych 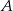 i
i 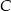 o mierze
o mierze 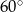 . Przekątna graniastosłupa
. Przekątna graniastosłupa 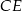 jest nachylona do płaszczyzny podstawy pod kątem
jest nachylona do płaszczyzny podstawy pod kątem 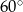 . Sporządź rysunek pomocniczy i zaznacz na nim wymienione w zadaniu kąty. Oblicz objętość tego graniastosłupa.
. Sporządź rysunek pomocniczy i zaznacz na nim wymienione w zadaniu kąty. Oblicz objętość tego graniastosłupa.
Rozwiązanie
Zacznijmy od rysunku.
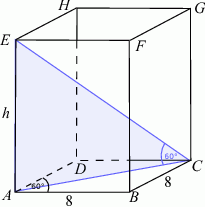
Aby obliczyć objętość graniastosłupa, potrzebujemy pole jego podstawy oraz wysokość. Pole podstawy obliczymy ze wzoru na pole rombu, gdy dany jest jego kąt:
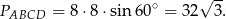
Wzór ten łatwo wynika ze wzoru na pole trójkąta 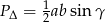 , gdzie
, gdzie 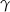 kąt między bokami
kąt między bokami  i
i 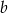 . Korzystając z tego wzoru możemy również wyliczyć długość odcinka
. Korzystając z tego wzoru możemy również wyliczyć długość odcinka 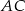 :
:
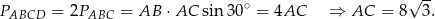
Długość odcinka 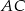 mogliśmy też wyliczyć z twierdzenia sinusów zastosowanego do trójkąta
mogliśmy też wyliczyć z twierdzenia sinusów zastosowanego do trójkąta 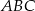 .
.
Aby obliczyć wysokość 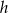 , zauważmy, że
, zauważmy, że 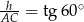 , stąd
, stąd
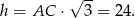
Zatem objętość graniastosłupa wynosi:
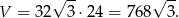
Odpowiedź: