/Szkoła średnia/Zadania maturalne
Egzamin Maturalny
z Matematyki (termin dodatkowy)
formuła 2015
poziom rozszerzony 11 czerwca 2024 Czas pracy: 180 minut
Zadania zamknięte
Liczba 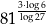 jest równa
jest równa
A) 6561 B) 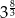 C) 1296 D)
C) 1296 D) 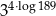
Liczba 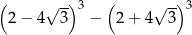 jest równa
jest równa
A) 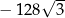 B)
B) 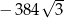 C)
C) 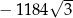 D)
D) 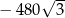
W trójkącie 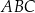 bok
bok 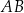 ma długość
ma długość 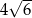 . Ponadto
. Ponadto 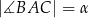 ,
, 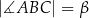 oraz
oraz 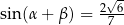 . Długość okręgu opisanego na trójkącie
. Długość okręgu opisanego na trójkącie 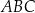 jest równa
jest równa
A) 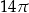 B)
B) 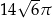 C)
C) 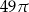 D)
D) 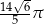
Funkcja 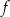 jest określona wzorem
jest określona wzorem 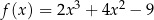 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Prosta o równaniu
. Prosta o równaniu 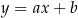 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 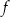 w punkcie
w punkcie 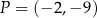 . Współczynnik
. Współczynnik  w równaniu tej stycznej jest równy
w równaniu tej stycznej jest równy
A) 8 B) 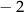 C)
C) 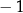 D)
D) 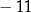
Zadania otwarte
Oblicz granicę 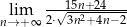 .
.
Doświadczenie losowe polega na dziesięciokrotnym rzucie symetryczną monetą. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w tym doświadczeniu losowym orzeł wypadł dokładnie trzy razy z rzędu, jeśli wiadomo, że wypadł dokładnie trzy razy.
Wykaż, że dla każdej liczby dodatniej  i każdej liczby dodatniej
i każdej liczby dodatniej 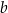 takich, że
takich, że 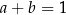 , prawdziwa jest nierówność
, prawdziwa jest nierówność
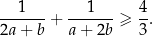
Długości podstaw trapezu równoramiennego są równe  oraz
oraz 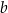 , przy czym
, przy czym 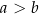 . W ten trapez można wpisać okrąg. Wykaż, że pole tego trapezu jest większe od
. W ten trapez można wpisać okrąg. Wykaż, że pole tego trapezu jest większe od 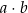 .
.
Nieskończony ciąg geometryczny 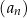 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 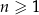 . Suma wszystkich wyrazów ciągu
. Suma wszystkich wyrazów ciągu 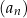 o numerach nieparzystych jest równa 16, tj.
o numerach nieparzystych jest równa 16, tj.
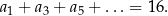
Ponadto 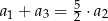 . Wyznacz wzór ogólny na n–ty wyraz ciągu
. Wyznacz wzór ogólny na n–ty wyraz ciągu 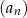 .
.
W okrąg o promieniu 4 wpisano trójkąt 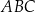 . Długość boku
. Długość boku 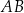 jest równa 6. Bok
jest równa 6. Bok 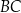 ma długość
ma długość 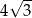 i jest najdłuższym bokiem tego trójkąta. Oblicz długość boku
i jest najdłuższym bokiem tego trójkąta. Oblicz długość boku 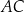 trójkąta
trójkąta 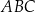 .
.
Rozwiąż równanie 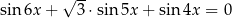 .
.
Długość krawędzi podstawy graniastosłupa prawidłowego trójkątnego jest równa  . Sinus kąta między przekątnymi ścian bocznych wychodzącymi z jednego wierzchołka
. Sinus kąta między przekątnymi ścian bocznych wychodzącymi z jednego wierzchołka 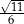 . Wyznacz pole powierzchni całkowitej tego graniastosłupa.
. Wyznacz pole powierzchni całkowitej tego graniastosłupa.
W kartezjańskim układzie współrzędnych 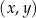 prosta o równaniu
prosta o równaniu 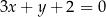 przecina parabolę o równaniu
przecina parabolę o równaniu 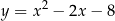 w punktach
w punktach 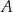 oraz
oraz 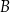 , które są kolejnymi wierzchołkami równoległoboku
, które są kolejnymi wierzchołkami równoległoboku 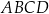 . Wierzchołek
. Wierzchołek 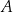 ma pierwszą współrzędną ujemną. Wierzchołek
ma pierwszą współrzędną ujemną. Wierzchołek 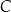 leży na prostej o równaniu
leży na prostej o równaniu 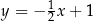 i ma pierwszą współrzędną dodatnią. Odległość punktu
i ma pierwszą współrzędną dodatnią. Odległość punktu 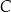 od prostej zawierającej bok
od prostej zawierającej bok 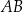 równoległoboku jest równa
równoległoboku jest równa 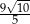 . Oblicz długość boku
. Oblicz długość boku 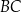 tego równoległoboku.
tego równoległoboku.
Wyznacz wszystkie wartości parametru 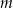 , dla których równanie
, dla których równanie
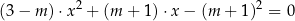
ma dwa różne rozwiązania rzeczywiste 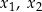 spełniające warunek
spełniające warunek
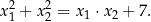
Rozpatrujemy wszystkie trapezy równoramienne, w których każda z przekątnych ma długość 10. Niech  oznacza długość odcinka łączącego środki ramion trapezu.
oznacza długość odcinka łączącego środki ramion trapezu.
-
Wykaż, że pole
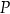 trapezu jako funkcja długości
trapezu jako funkcja długości  odcinka łączącego środki ramion trapezu jest określone wzorem
odcinka łączącego środki ramion trapezu jest określone wzorem 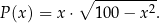
-
Wyznacz dziedzinę funkcji
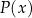 .
. -
Oblicz długość
 odcinka łączącego środki ramion tego z rozpatrywanych trapezów, którego pole jest największe. Oblicz to największe pole.
odcinka łączącego środki ramion tego z rozpatrywanych trapezów, którego pole jest największe. Oblicz to największe pole.

