/Szkoła średnia/Zadania maturalne
Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom rozszerzony 3 czerwca 2016 Czas pracy: 180 minut
Zadania zamknięte
Funkcja 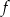 określona jest wzorem
określona jest wzorem 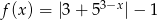 dla każdej liczby rzeczywistej. Zbiorem wartości funkcji
dla każdej liczby rzeczywistej. Zbiorem wartości funkcji 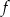 jest
jest
A) 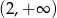 B)
B) 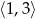 C)
C) 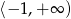 D)
D) 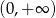
Wartość wyrażenia 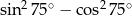 jest równa
jest równa
A) 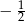 B)
B) 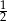 C)
C) 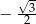 D)
D) 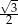
W trapezie 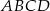 o podstawach
o podstawach 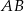 i
i 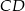 dane są:
dane są: 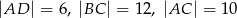 oraz
oraz 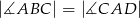 (zobacz rysunek).
(zobacz rysunek).
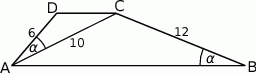
Wówczas długość podstawy 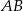 tego trapezu jest równa
tego trapezu jest równa
A) 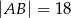 B)
B) 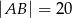 C)
C) 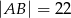 D)
D) 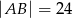
W ostrosłupie prawidłowym czworokątnym wszystkie krawędzie mają jednakową długość. Wynika stąd, że cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa jest równy
A) 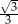 B)
B) 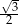 C)
C) 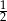 D)
D) 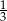
Granica 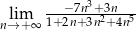 jest równa
jest równa
A) 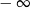 B)
B) 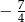 C) 0 D)
C) 0 D) 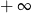
Zadania otwarte
Dany jest nieskończony ciąg geometryczny 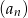 określony dla
określony dla 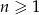 , w którym iloraz jest równy pierwszemu wyrazowi, a suma wszystkich wyrazów tego ciągu jest równa 12. Oblicz pierwszy wyraz tego ciągu.
, w którym iloraz jest równy pierwszemu wyrazowi, a suma wszystkich wyrazów tego ciągu jest równa 12. Oblicz pierwszy wyraz tego ciągu.
Dane są zdarzenia losowe 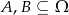 takie, że
takie, że 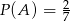 i
i 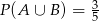 . Oblicz
. Oblicz 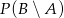 , gdzie zdarzenie
, gdzie zdarzenie 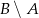 oznacza różnicę zdarzeń
oznacza różnicę zdarzeń 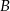 i
i 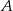 .
.
Wykaż, że dla 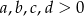 prawdziwa jest nierówność
prawdziwa jest nierówność 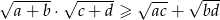 .
.
Rozwiąż nierówność 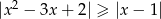 .
.
Dany jest ciąg 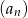 określony dla każdej liczby całkowitej
określony dla każdej liczby całkowitej 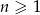 , w którym
, w którym 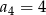 oraz dla każdej liczby
oraz dla każdej liczby 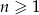 prawdziwa jest równość
prawdziwa jest równość 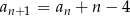 . Oblicz pierwszy wyraz ciągu
. Oblicz pierwszy wyraz ciągu 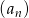 i ustal, czy ciąg ten jest malejący.
i ustal, czy ciąg ten jest malejący.
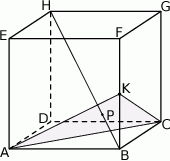
Dany jest sześcian 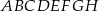 . Przez wierzchołki
. Przez wierzchołki 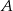 i
i 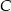 oraz środek
oraz środek 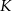 krawędzi
krawędzi 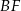 poprowadzono płaszczyznę, która przecina przekątną
poprowadzono płaszczyznę, która przecina przekątną 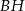 w punkcie
w punkcie 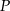 (zobacz rysunek).
(zobacz rysunek).
Wykaż, że 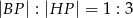 .
.
Liczba 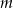 jest sumą odwrotności dwóch różnych pierwiastków równania
jest sumą odwrotności dwóch różnych pierwiastków równania
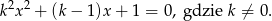
Wyznacz zbiór wartości funkcji określonej wzorem 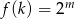 .
.
Rozwiąż nierówność 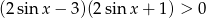 w przedziale
w przedziale 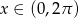 .
.
W trójkącie prostokątnym stosunek różnicy długości przyprostokątnych do długości przeciwprostokątnej jest równy 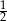 . Oblicz cosinusy kątów ostrych tego trójkąta.
. Oblicz cosinusy kątów ostrych tego trójkąta.
Oblicz, ile jest wszystkich liczb naturalnych pięciocyfrowych, w których zapisie występują dokładnie trzy cyfry nieparzyste.
Punkty 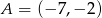 i
i 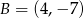 są wierzchołkami podstawy trójkąta równoramiennego
są wierzchołkami podstawy trójkąta równoramiennego  , a wysokość opuszczona z wierzchołka
, a wysokość opuszczona z wierzchołka  tego trójkąta zawiera się w prostej o równaniu
tego trójkąta zawiera się w prostej o równaniu 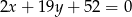 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 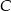 .
.
Rozpatrujemy wszystkie walce, których pole powierzchni całkowitej jest równe 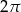 . Oblicz promień podstawy tego walca, który ma największą objętość. Podaj tę największą objętość.
. Oblicz promień podstawy tego walca, który ma największą objętość. Podaj tę największą objętość.

