/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 17 kwietnia 2021 Czas pracy: 180 minut
Zadania zamknięte
Liczba 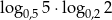 jest równa
jest równa
A) 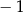 B) 1 C) 10 D) 0,1
B) 1 C) 10 D) 0,1
Ciąg 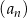 jest określony wzorem
jest określony wzorem 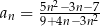 dla każdej liczby
dla każdej liczby 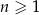 . Granica tego ciągu jest równa
. Granica tego ciągu jest równa
A) 5 B) 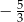 C)
C) 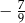 D)
D) 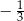
Prosta dana równaniem 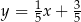 jest prostopadła do stycznej do wykresu funkcji
jest prostopadła do stycznej do wykresu funkcji 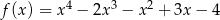 w punkcie
w punkcie
A) 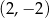 B)
B) 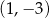 C)
C) 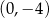 D)
D) 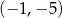
Wskaż wektor równoległy do wektora ![→ v = [− 72,96 ]](https://img.zadania.info/zes/0051973/HzesT14x.gif)
A) ![[48,36]](https://img.zadania.info/zes/0051973/HzesT15x.gif) B)
B) ![[45,− 60 ]](https://img.zadania.info/zes/0051973/HzesT16x.gif) C)
C) ![[− 42,64]](https://img.zadania.info/zes/0051973/HzesT17x.gif) D)
D) ![[76,− 57 ]](https://img.zadania.info/zes/0051973/HzesT18x.gif)
Zadania otwarte
Dwa zakłady pracy produkują takie same akumulatory, przy czym stosunek liczby akumulatorów produkowanych dziennie przez pierwszy zakład do liczby akumulatorów produkowanych dziennie przez drugi zakład jest równy  . Badania wykazały, że niektóre z wyprodukowanych akumulatorów mają podwyższoną pojemność, przy czym własność tą ma 40% akumulatorów pochodzących z pierwszego zakładu i 30% akumulatorów pochodzących z drugiego zakładu. Oblicz jakie jest prawdopodobieństwo, że losowo wybrany akumulator pochodzący z dziennej produkcji obu zakładów nie ma podwyższonej pojemności.
. Badania wykazały, że niektóre z wyprodukowanych akumulatorów mają podwyższoną pojemność, przy czym własność tą ma 40% akumulatorów pochodzących z pierwszego zakładu i 30% akumulatorów pochodzących z drugiego zakładu. Oblicz jakie jest prawdopodobieństwo, że losowo wybrany akumulator pochodzący z dziennej produkcji obu zakładów nie ma podwyższonej pojemności.
Wyznacz wszystkie wartości parametru 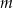 , dla których równanie
, dla których równanie
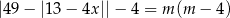
ma cztery różne rozwiązania, których iloczyn jest ujemny.
Suma długości wszystkich wysokości trójkąta 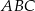 jest 9 razy większa od promienia okręgu wpisanego w ten trójkąt. Udowodnij, że trójkąt
jest 9 razy większa od promienia okręgu wpisanego w ten trójkąt. Udowodnij, że trójkąt 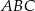 jest równoboczny.
jest równoboczny.
Wykaż, że 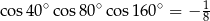 .
.
Okrąg wpisany w trójkąt 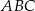 jest opisany równaniem
jest opisany równaniem
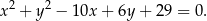
Punkty styczności tego okręgu z bokami 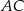 i
i 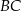 trójkąta
trójkąta 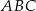 leżą na prostej o równaniu:
leżą na prostej o równaniu: 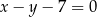 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 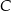 trójkąta
trójkąta 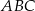 .
.
Wykres funkcji 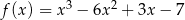 przesunięto o wektor
przesunięto o wektor 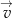 i wyniku tej operacji otrzymano wykres, który jest symetryczny względem początku układu współrzędnych. Wyznacz współrzędne wektora
i wyniku tej operacji otrzymano wykres, który jest symetryczny względem początku układu współrzędnych. Wyznacz współrzędne wektora 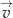 .
.
W trzywyrazowym ciągu geometrycznym 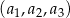 spełniona jest równość
spełniona jest równość  . Wyrazy
. Wyrazy 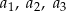 są – odpowiednio – dziewiątym, trzecim i pierwszym wyrazem rosnącego ciągu arytmetycznego. Oblicz
są – odpowiednio – dziewiątym, trzecim i pierwszym wyrazem rosnącego ciągu arytmetycznego. Oblicz 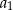 .
.
Czworokąt 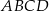 jest wpisany w okrąg o promieniu
jest wpisany w okrąg o promieniu 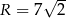 . Kąt
. Kąt 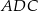 tego czworokąta jest ostry i jego miara jest o
tego czworokąta jest ostry i jego miara jest o 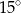 większa od miary kąta
większa od miary kąta 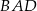 . Iloczyn sinusów wszystkich kątów wewnętrznych czworokąta
. Iloczyn sinusów wszystkich kątów wewnętrznych czworokąta 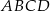 jest równy
jest równy  . Oblicz długości przekątnych
. Oblicz długości przekątnych 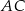 i
i 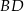 tego czworokąta.
tego czworokąta.
Reszta z dzielenia wielomianu 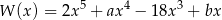 przez trójmian
przez trójmian 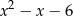 jest równa
jest równa 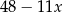 . Oblicz resztę z dzielenia wielomianu
. Oblicz resztę z dzielenia wielomianu 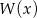 przez trójmian
przez trójmian 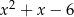 .
.
Przez punkt 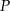 krawędzi bocznej
krawędzi bocznej 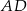 graniastosłupa prawidłowego trójkątnego
graniastosłupa prawidłowego trójkątnego 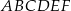 o krawędzi podstawy równej
o krawędzi podstawy równej  poprowadzono dwie płaszczyzny. Jedna przechodzi przez przeciwległą krawędź dolnej podstawy i jest nachylona do tej podstawy pod kątem
poprowadzono dwie płaszczyzny. Jedna przechodzi przez przeciwległą krawędź dolnej podstawy i jest nachylona do tej podstawy pod kątem  , a druga przechodzi przez przeciwległą krawędź górnej podstawy i jest nachylona do tej podstawy pod kątem
, a druga przechodzi przez przeciwległą krawędź górnej podstawy i jest nachylona do tej podstawy pod kątem 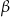 (zobacz rysunek).
(zobacz rysunek).
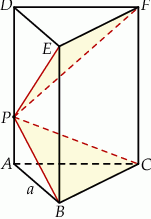
Udowodnij, że objętość ostrosłupa 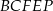 jest równa
jest równa
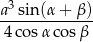
Mówimy, że walec jest wpisany w graniastosłup, jeżeli podstawy walca są zawarte w podstawach graniastosłupa, a powierzchnia boczna walca jest styczna do każdej ze ścian bocznych graniastosłupa (zobacz rysunek).
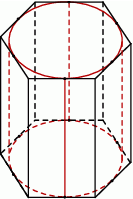
Rozpatrujemy wszystkie graniastosłupy prawidłowe sześciokątne takie, że suma długości promienia i wysokości walca wpisanego w ten graniastosłup jest równa 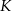 . Oblicz pole powierzchni całkowitej tego z rozważanych graniastosłupów, którego objętość jest największa.
. Oblicz pole powierzchni całkowitej tego z rozważanych graniastosłupów, którego objętość jest największa.

