/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 9 kwietnia 2011 Czas pracy: 180 minut
Rozwiąż równanie 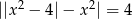 .
.
Wyznacz równanie okręgu, który jest symetryczny do okręgu o równaniu
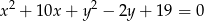
względem prostej 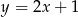 .
.
Rozwiąż nierówność
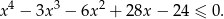
W trapezie 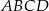 podstawa
podstawa 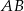 jest 3 razy dłuższa od podstawy
jest 3 razy dłuższa od podstawy 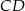 . Przekątne tego trapezu przecinają się w punkcie
. Przekątne tego trapezu przecinają się w punkcie 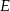 , a proste zawierające ramiona
, a proste zawierające ramiona 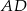 i
i 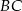 przecinają się w punkcie
przecinają się w punkcie 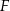 . Oblicz stosunek pola czworokąta
. Oblicz stosunek pola czworokąta 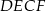 do pola trapezu
do pola trapezu 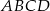 .
.
Ciąg 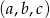 jest geometryczny, a ciągi
jest geometryczny, a ciągi 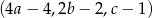 i
i 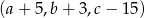 są arytmetyczne. Oblicz
są arytmetyczne. Oblicz 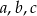 .
.
- Wykaż, że dla dowolnych liczb nieujemnych
 i
i 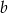 spełniona jest nierówność
spełniona jest nierówność 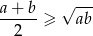
- W zbiorze prostokątów wpisanych w okrąg o promieniu
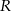 znajdź prostokąt o największym polu.
znajdź prostokąt o największym polu.
Dany jest trójkąt równoramienny 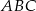 , w którym
, w którym 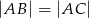 i
i 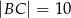 . Na boku
. Na boku 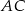 wybrano punkt
wybrano punkt 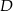 w ten sposób, że
w ten sposób, że 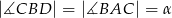 oraz
oraz 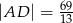 . Oblicz
. Oblicz 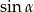 .
.
Liczby 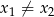 są dwoma dodatnimi pierwiastkami równania
są dwoma dodatnimi pierwiastkami równania 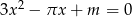 z niewiadomą
z niewiadomą  , gdzie
, gdzie 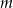 jest pewną ustaloną liczbą rzeczywistą.
jest pewną ustaloną liczbą rzeczywistą.
- Wykaż, że
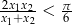 .
. - Wykaż, że
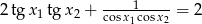 .
.
Oblicz prawdopodobieństwo, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb wyrzuconych oczek będzie podzielna przez 4.
Podstawą ostrosłupa 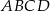 jest trójkąt
jest trójkąt 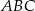 , a krawędź
, a krawędź 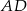 jest wysokością ostrosłupa. Oblicz pole powierzchni całkowitej ostrosłupa
jest wysokością ostrosłupa. Oblicz pole powierzchni całkowitej ostrosłupa 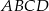 , jeśli wiadomo, że jego objętość jest równa 48 oraz
, jeśli wiadomo, że jego objętość jest równa 48 oraz 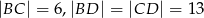 . Podaj wszystkie możliwe odpowiedzi.
. Podaj wszystkie możliwe odpowiedzi.

