/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki (CEN Bydgoszcz)
poziom rozszerzony 10 marca 2014 Czas pracy: 170 minut
Rozwiąż nierówność 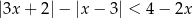 .
.
Udowodnij, że dla 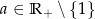 oraz
oraz 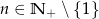 spełniona jest równość:
spełniona jest równość:
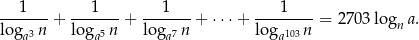
Punkty 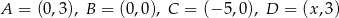 , gdzie
, gdzie 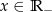 są kolejnymi wierzchołkami czworokąta
są kolejnymi wierzchołkami czworokąta 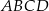 . Oblicz wartość
. Oblicz wartość  , dla której w czworokąt
, dla której w czworokąt 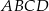 można wpisać okrąg.
można wpisać okrąg.
Napisz wzór i naszkicuj wykres funkcji 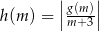 wiedząc, że funkcja
wiedząc, że funkcja 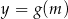 każdej liczbie rzeczywistej
każdej liczbie rzeczywistej 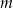 przyporządkowuje najmniejszą wartość funkcji kwadratowej
przyporządkowuje najmniejszą wartość funkcji kwadratowej 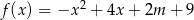 w przedziale
w przedziale 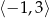 .
.
Graniastosłup prawidłowy czworokątny o krawędzi podstawy 6 cm przecięto płaszczyzną przechodzącą przez środki dwóch sąsiednich krawędzi podstawy. Płaszczyzna ta przecina trzy krawędzie boczne i jest nachylona do płaszczyzny podstawy pod kątem 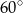 . Zaznacz na rysunku ten przekrój i oblicz jego pole.
. Zaznacz na rysunku ten przekrój i oblicz jego pole.
Dany jest ciąg określony rekurencyjnie
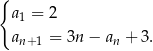
Wyznacz liczby całkowite 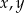 tak, aby ciąg
tak, aby ciąg 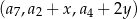 był ciągiem arytmetycznym, natomiast ciąg
był ciągiem arytmetycznym, natomiast ciąg 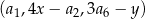 był ciągiem geometrycznym.
był ciągiem geometrycznym.
Rozwiąż równanie 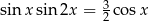 w przedziale
w przedziale 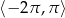 .
.
Wykaż, że jeżeli 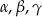 są kątami wewnętrznymi trójkąta i
są kątami wewnętrznymi trójkąta i 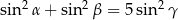 , to
, to 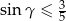 .
.
Wykres funkcji wykładniczej 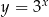 przekształcono i otrzymano wykres funkcji
przekształcono i otrzymano wykres funkcji 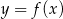 (rys).
(rys).
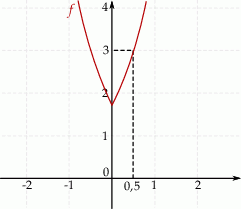
Napisz wzór funkcji 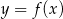 , a następnie zaznacz na płaszczyźnie zbiór
, a następnie zaznacz na płaszczyźnie zbiór
![{ } A = x,y : x ∈ R i y ∈ R i log(x−1)2+y 2[log 9f2(x)] < 0 .](https://img.zadania.info/zes/0057488/HzesT28x.gif)
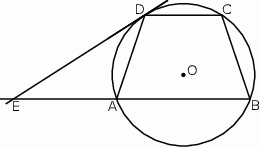
W okrąg wpisano trapez równoramienny 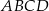 , którego podstawy mają długości:
, którego podstawy mają długości: 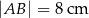 ,
, 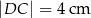 . Styczna do okręgu w punkcie
. Styczna do okręgu w punkcie 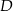 przecina prostą
przecina prostą 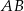 w punkcie
w punkcie 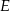 (rys). Wiedząc, że
(rys). Wiedząc, że 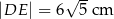 oblicz promień okręgu opisanego na trapezie
oblicz promień okręgu opisanego na trapezie 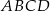 .
.
Pięć ponumerowanych kul rozmieszczamy losowo w czterech ponumerowanych szufladach. Oblicz ile jest możliwości takiego rozmieszczenia kul, aby dokładnie dwie szuflady były puste.
Dla jakich wartości 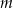 reszta z dzielenia wielomianu
reszta z dzielenia wielomianu 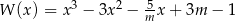 przez dwumian
przez dwumian 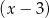 jest niewiększa od 3?
jest niewiększa od 3?

