/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 9 marca 2024 Czas pracy: 180 minut
Dane są liczby
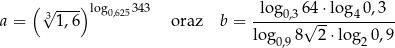
Oblicz 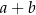 .
.
Oblicz granicę jednostronną
Oblicz, ile jest wszystkich liczb naturalnych sześciocyfrowych, w których zapisie dziesiętnym dokładnie trzy razy występuje cyfra 1.
Kasia i Ula grają w warcaby i każda rozgrywka kończy się wygraną jednej z dziewczynek. Prawdopodobieństwo wygrania pojedynczej partii przez Ulę jest równe 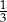 . Oblicz prawdopodobieństwo wygrania przez Kasię co najmniej sześciu z siedmiu rozegranych partii. Wynik podaj w postaci ułamka zwykłego nieskracalnego.
. Oblicz prawdopodobieństwo wygrania przez Kasię co najmniej sześciu z siedmiu rozegranych partii. Wynik podaj w postaci ułamka zwykłego nieskracalnego.
Rozwiąż równanie 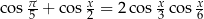 .
.
Wykaż, że dla każdej liczby rzeczywistej dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność
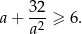
W okrąg o promieniu 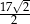 wpisano czworokąt
wpisano czworokąt 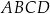 tak, że
tak, że 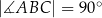 oraz
oraz 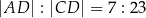 . Oblicz obwód czworokąta
. Oblicz obwód czworokąta 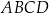 jeżeli jego pole jest równe 192.
jeżeli jego pole jest równe 192.
Określamy kwadraty 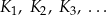 następująco:
następująco:
-
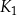 jest kwadratem o boku długości
jest kwadratem o boku długości 
-
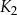 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 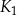 i dzieli ten bok w stosunku 1 : 2
i dzieli ten bok w stosunku 1 : 2 -
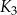 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 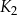 i dzieli ten bok w stosunku 1 : 2
i dzieli ten bok w stosunku 1 : 2
i ogólnie, dla każdej liczby naturalnej 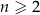 ,
,
-
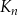 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 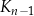 i dzieli ten bok w stosunku 1 : 2.
i dzieli ten bok w stosunku 1 : 2.
Obwody wszystkich kwadratów określonych powyżej tworzą nieskończony ciąg geometryczny. Na rysunku przedstawiono kwadraty utworzone w sposób opisany powyżej.
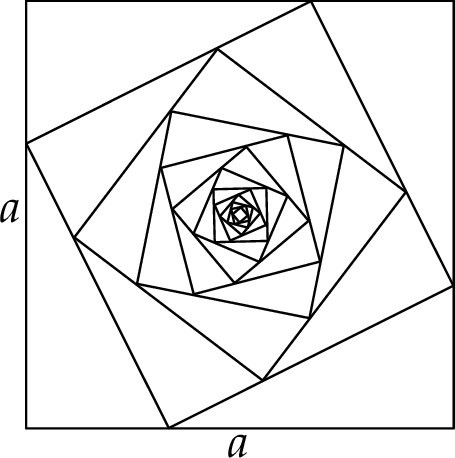
Oblicz sumę wszystkich wyrazów tego nieskończonego ciągu.
Wyznacz pierwsze trzy wyrazy ciągu geometrycznego wiedząc, że ich suma jest równa 10,5 oraz suma ich kwadratów jest równa 47,25.
W okrąg o równaniu 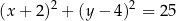 wpisano trójkąt
wpisano trójkąt 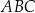 , którego pole jest równe 20. Bok
, którego pole jest równe 20. Bok 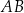 tego trójkąta jest zawarty w prostej o równaniu
tego trójkąta jest zawarty w prostej o równaniu 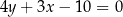 , a wysokość opuszczona z wierzchołka
, a wysokość opuszczona z wierzchołka 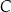 przecina bok
przecina bok 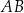 w punkcie
w punkcie 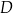 , którego obie współrzędne są dodatnie. Oblicz współrzędne punktu
, którego obie współrzędne są dodatnie. Oblicz współrzędne punktu 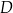 .
.
Dany jest graniastosłup prosty 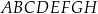 o podstawie prostokątnej
o podstawie prostokątnej 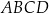 . Przekątne
. Przekątne 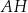 ,
, 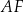 i
i 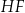 ścian bocznych tworzą trójkąt ostrokątny o polu 11,25 (zobacz rysunek). Stosunek długości odcinka
ścian bocznych tworzą trójkąt ostrokątny o polu 11,25 (zobacz rysunek). Stosunek długości odcinka 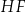 do promienia okręgu opisanego na trójkącie
do promienia okręgu opisanego na trójkącie 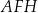 jest równy 30 : 17. Oblicz wysokość
jest równy 30 : 17. Oblicz wysokość 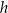 tego graniastosłupa.
tego graniastosłupa.
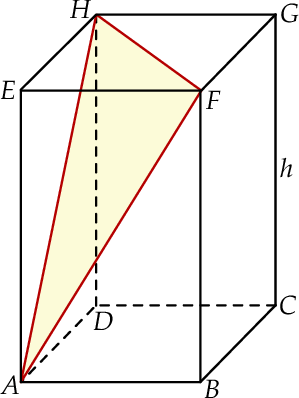
Wyznacz wszystkie wartości parametru 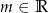 , dla których równanie
, dla których równanie
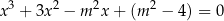
ma trzy różne pierwiastki, z których jeden jest ujemny, a pozostałe dwa należą do przedziału ![[ ] 1 2 ,5](https://img.zadania.info/zes/0060936/HzesT42x.png) .
.
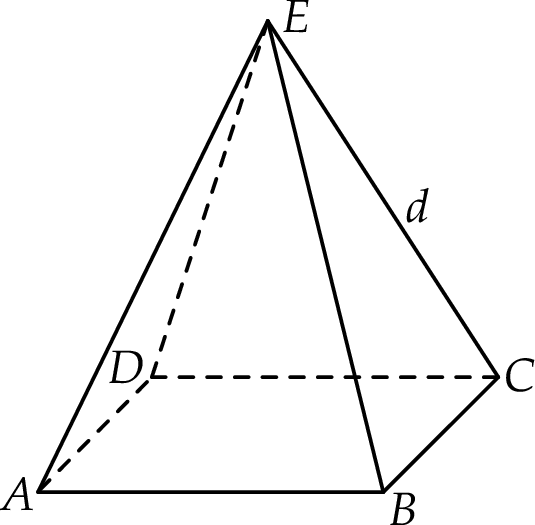
Rozważamy wszystkie ostrosłupy prawidłowe czworokątne 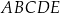 , w których krawędź boczna ma długość
, w których krawędź boczna ma długość 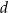 (zobacz rysunek).
(zobacz rysunek).
-
Wyznacz zależność objętości
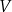 ostrosłupa od jego wysokości
ostrosłupa od jego wysokości 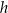 i podaj dziedzinę funkcji
i podaj dziedzinę funkcji 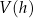 .
. -
Wyznacz wysokość tego z rozważanych ostrosłupów, którego objętość jest największa.

