/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 2 marca 2024 Czas pracy: 180 minut
W chwili początkowej masa substancji jest równa 20 g. Wskutek rozpadu cząsteczek tej substancji jej masa się zmniejsza. Po każdej kolejnej dobie ubywa 20% masy, jaka była na koniec doby poprzedniej. Oblicz, po ilu pełnych dobach masa tej substancji będzie po raz pierwszy mniejsza od 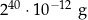 .
.
Karol i Antek grają w rzutki. Karol trafia w środek tarczy z prawdopodobieństwem 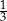 , a Antek z prawdopodobieństwem
, a Antek z prawdopodobieństwem  . Rzucamy symetryczną, sześcienną kostką do gry. Jeżeli wypadnie liczba podzielna przez 3, to Karol dwa razy rzuca do tarczy. W przeciwnym wypadku Antek dwa razy rzuca do tarczy. Oblicz prawdopodobieństwa zdarzenia polegającego na tym, że w żadnym z tych dwóch wykonanych rzutów nie zostanie trafiony środek tarczy.
. Rzucamy symetryczną, sześcienną kostką do gry. Jeżeli wypadnie liczba podzielna przez 3, to Karol dwa razy rzuca do tarczy. W przeciwnym wypadku Antek dwa razy rzuca do tarczy. Oblicz prawdopodobieństwa zdarzenia polegającego na tym, że w żadnym z tych dwóch wykonanych rzutów nie zostanie trafiony środek tarczy.
Wykaż, że jeżeli pierwiastkiem wielomianu
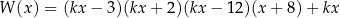
jest liczba całkowita podzielna przez 5, to 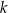 nie jest liczbą całkowitą.
nie jest liczbą całkowitą.
Oblicz granicę ciągu
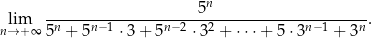
Dany jest kwadrat 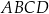 o boku długości 3. Punkty
o boku długości 3. Punkty 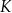 i
i 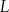 leżą na prostych – odpowiednio –
leżą na prostych – odpowiednio – 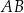 i
i 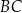 tak, że
tak, że 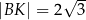 i
i 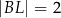 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 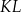 przecina przekątną
przecina przekątną 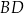 tego kwadratu w punkcie
tego kwadratu w punkcie 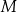 .
.
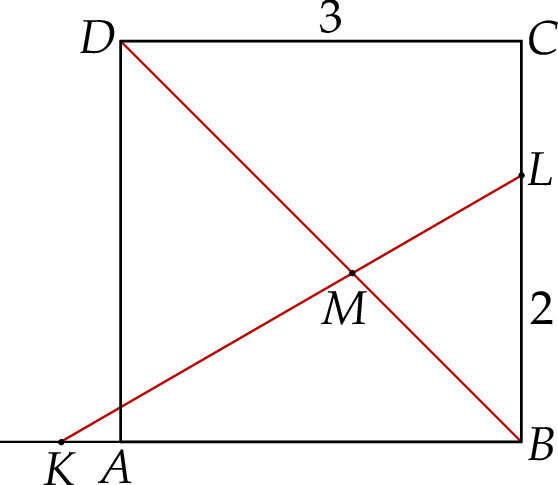
Wykaż, że 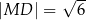 .
.
Funkcja 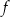 jest określona wzorem
jest określona wzorem 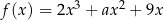 dla każdego
dla każdego 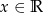 , i ustalonej liczby rzeczywistej
, i ustalonej liczby rzeczywistej  . Prosta
. Prosta 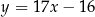 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 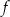 . Oblicz
. Oblicz  .
.
Rozwiąż równanie 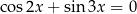 w zbiorze
w zbiorze ![[ ] − π2-, π2](https://img.zadania.info/zes/0061844/HzesT26x.png) .
.
Rozwiąż nierówność 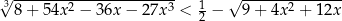 .
.
Przekątne czworokąta wypukłego 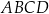 wpisanego w okrąg przecinają się w punkcie
wpisanego w okrąg przecinają się w punkcie 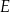 tak, że
tak, że 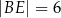 ,
, 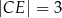 i
i 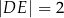 . Ponadto
. Ponadto 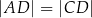 (zobacz rysunek).
(zobacz rysunek).

Oblicz długości boków czworokąta 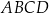 oraz promień opisanego na nim okręgu.
oraz promień opisanego na nim okręgu.
Oblicz długość odcinka łączącego środki przeciwległych krawędzi czworościanu foremnego o krawędzi długości  .
.
Informacja do zadań 11.1 i 11.2
Funkcja kwadratowa 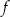 określona jest wzorem
określona jest wzorem 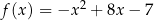 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej  .
.
Parabola będąca wykresem funkcji 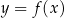 przecina prostą
przecina prostą 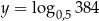 w punktach
w punktach 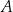 i
i 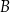 . Wykaż, że suma kwadratów pierwszych współrzędnych punktów
. Wykaż, że suma kwadratów pierwszych współrzędnych punktów 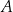 i
i 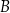 jest równa
jest równa 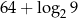 .
.
Na paraboli 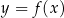 znajdź taki punkt
znajdź taki punkt 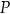 , który leży powyżej osi
, który leży powyżej osi 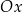 , i dla którego stosunek jego pierwszej współrzędnej do drugiej jest najmniejszy możliwy.
, i dla którego stosunek jego pierwszej współrzędnej do drugiej jest najmniejszy możliwy.
W kartezjańskim układzie współrzędnych 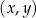 prosta
prosta 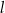 o równaniu
o równaniu 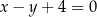 przecina parabolę o równaniu
przecina parabolę o równaniu 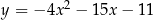 w punktach
w punktach 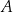 oraz
oraz 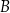 . Odcinek
. Odcinek 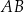 jest średnicą okręgu
jest średnicą okręgu 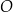 . Punkt
. Punkt 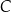 leży na okręgu
leży na okręgu 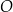 poniżej prostej
poniżej prostej 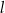 , a kąt
, a kąt 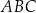 jest ostry i ma miarę
jest ostry i ma miarę  taką, że
taką, że 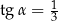 (zobacz rysunek).
(zobacz rysunek).
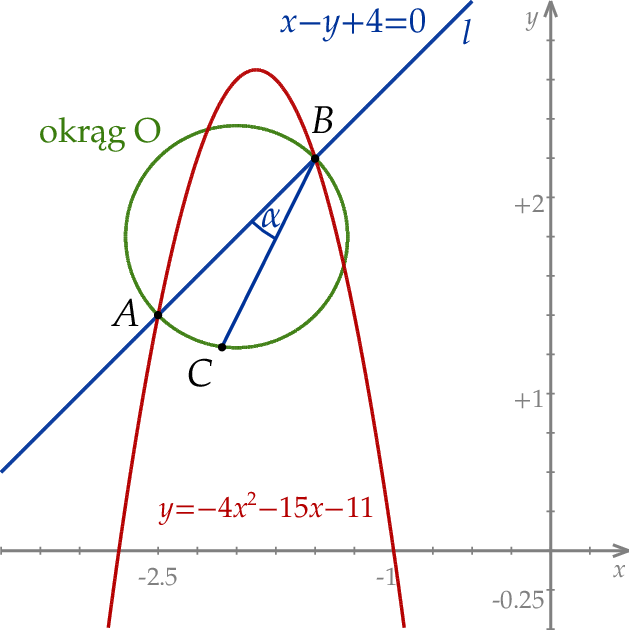
Oblicz współrzędne punktu 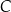 .
.

