/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 4 kwietnia 2020 Czas pracy: 170 minut
Zadania zamknięte
Liczba 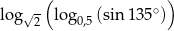 jest równa
jest równa
A) 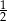 B)
B) 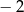 C) 2 D)
C) 2 D) 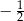
Liczba naturalna 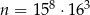 w zapisie dziesiętnym ma
w zapisie dziesiętnym ma
A) 14 cyfr B) 15 cyfr C) 11 cyfr D) 8 cyfr
Liczba 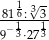 jest równa
jest równa
A) 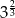 B)
B) 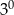 C)
C) 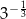 D)
D) 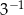
W trakcie testów drogowych samochód numer 1 poruszał się ze stałą prędkością 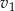 i pokonał trasę o 20% dłuższą, niż samochód nr 2, który poruszał się ze stałą prędkością
i pokonał trasę o 20% dłuższą, niż samochód nr 2, który poruszał się ze stałą prędkością 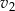 . Czas w jakim samochód nr 2 pokonał swoją trasę był o 25% krótszy, niż czas w jakim swoją trasę pokonał samochód nr 1. Stosunek prędkości
. Czas w jakim samochód nr 2 pokonał swoją trasę był o 25% krótszy, niż czas w jakim swoją trasę pokonał samochód nr 1. Stosunek prędkości 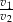 jest równy
jest równy
A) 1 B) 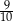 C)
C) 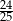 D)
D) 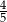
Para liczb 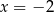 i
i 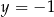 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 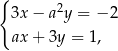 dla
dla
A) 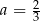 B)
B) 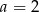 C)
C) 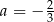 D)
D) 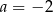
Równanie 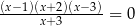
A) ma trzy różne rozwiązania: 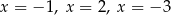 .
.
B) ma trzy różne rozwiązania: 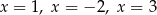 .
.
C) ma dwa różne rozwiązania: 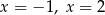 .
.
D) ma dwa różne rozwiązania: 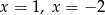 .
.
Do wykresu funkcji liniowej 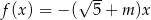 nie należy żaden punkt o obu współrzędnych dodatnich. Wynika stąd, że
nie należy żaden punkt o obu współrzędnych dodatnich. Wynika stąd, że
A) 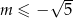 B)
B) 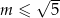 C)
C) 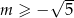 D)
D) 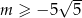
Na rysunku przedstawiono fragment paraboli będącej wykresem funkcji kwadratowej 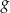 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 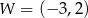 .
.
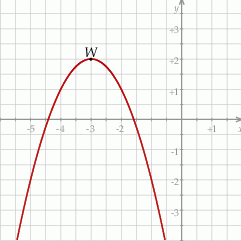
Zbiorem wartości funkcji 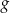 jest przedział
jest przedział
A) 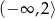 B)
B) 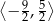 C)
C) 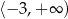 D)
D) 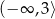
Miejscami zerowymi funkcji kwadratowej 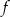 są liczby
są liczby 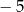 i 6, a miejscami zerowymi funkcji
i 6, a miejscami zerowymi funkcji 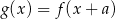 są liczby 1 i 12. Wynika stąd, że
są liczby 1 i 12. Wynika stąd, że
A) 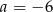 B)
B) 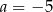 C)
C) 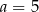 D)
D) 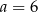
Zbiorem rozwiązań nierówności 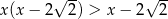 jest zbiór
jest zbiór
A) 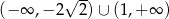 B)
B) 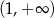
C) 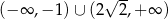 D)
D) 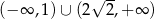
Wyrażenie 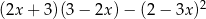 zapisać można w postaci
zapisać można w postaci
A) 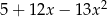 B)
B) 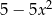 C)
C) 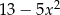 D)
D) 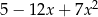
Dany jest nieskończony rosnący ciąg geometryczny 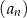 o wyrazach dodatnich. Iloraz
o wyrazach dodatnich. Iloraz 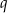 tego ciągu jest jednym z pierwiastków równania kwadratowego
tego ciągu jest jednym z pierwiastków równania kwadratowego 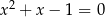 . Zatem wartość wyrażenia
. Zatem wartość wyrażenia
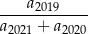
jest równa
A) 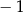 B)
B) 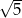 C)
C) 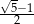 D) 1
D) 1
Dany jest ciąg arytmetyczny 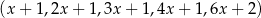 . Wtedy
. Wtedy
A) 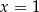 B)
B) 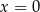 C)
C) 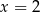 D)
D) 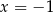
Wartość wyrażenia 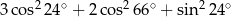 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
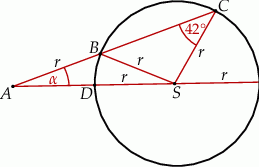
Punkty  i
i 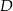 leżą na okręgu o środku
leżą na okręgu o środku 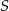 i promieniu
i promieniu  . Punkt
. Punkt 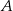 jest punktem wspólnym prostych
jest punktem wspólnym prostych 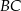 i
i 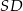 , a odcinki
, a odcinki 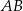 i
i 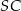 są równej długości. Miara kąta
są równej długości. Miara kąta 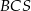 jest równa
jest równa 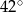 (zobacz rysunek). Wtedy
(zobacz rysunek). Wtedy
A)  B)
B)  C)
C) 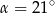 D)
D) 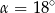
Dany jest romb o boku długości 4 i polu równym 8. Kąt rozwarty tego rombu ma miarę
A) 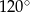 B)
B) 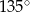 C)
C) 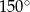 D)
D) 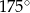
Proste o równaniach 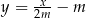 i
i 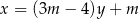 są równoległe, gdy
są równoległe, gdy
A) 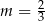 B)
B) 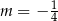 C)
C) 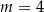 D)
D) 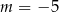
Boki równoległoboku są zawarte w prostych o równaniach: 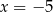 ,
, 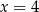 ,
, 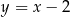 ,
, 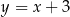 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 45 B) 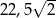 C)
C) 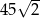 D) 22,5
D) 22,5
W układzie współrzędnych punkt 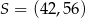 jest środkiem odcinka
jest środkiem odcinka 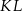 , którego jednym z końców jest punkt
, którego jednym z końców jest punkt 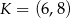 . Zatem
. Zatem
A) 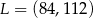 B)
B) 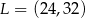 C)
C) 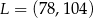 D)
D) 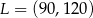
Dane są punkty o współrzędnych 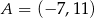 oraz
oraz 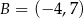 . Średnica okręgu wpisanego w sześciokąt foremny o boku
. Średnica okręgu wpisanego w sześciokąt foremny o boku 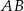 jest równa
jest równa
A) 10 B) 5 C) 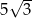 D)
D) 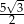
W grupie 50 kobiet i 50 mężczyzn przeprowadzono ankietę, w której zadano pytanie o liczbę książek przeczytanych w ostatnim roku. Wyniki ankiety zebrano w poniższej tabeli.
| Liczba książek | 0 | 1 | 2 | 3 | 4 | 5 |
| Liczba osób | 19 | 21 | 24 | 21 | 7 | 8 |
W trakcie analizy tych danych zauważono, że kobiety przeczytały średnio o dwie książki więcej niż mężczyźni. Średnia liczba przeczytanych książek przez jednego ankietowanego mężczyznę jest równa
A) 1,5 B) 1 C) 2 D) 2,5
Pole powierzchni całkowitej pewnego stożka jest 5 razy większe od pola powierzchni pewnej kuli. Promień tej kuli jest taki sam jak promień podstawy tego stożka. Tworząca tego stożka jest nachylona do podstawy pod kątem  takim, że
takim, że
A) 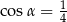 B)
B) 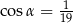 C)
C) 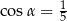 D)
D) 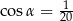
Podstawą ostrosłupa jest kwadrat 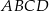 o boku długości 12. Krawędź boczna
o boku długości 12. Krawędź boczna 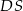 jest prostopadła do podstawy i ma długość 9 (zobacz rysunek).
jest prostopadła do podstawy i ma długość 9 (zobacz rysunek).
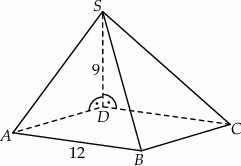
Pole ściany 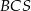 tego ostrosłupa jest równe
tego ostrosłupa jest równe
A) 180 B) 108 C) 54 D) 90
Wszystkich liczb czterocyfrowych parzystych, w których zapisie nie występują cyfry: 5, 2, 4, 8, 7, jest
A) 500 B) 625 C) 250 D) 200
W grupie 24 osób (mężczyzn i kobiet) jest 3 razy więcej kobiet niż mężczyzn. Z grupy tej losujemy 2 osoby. Prawdopodobieństwo wylosowania każdej osoby jest takie samo. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowano osoby różnej płci to
A) 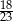 B)
B)  C)
C) 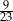 D)
D) 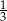
Zadania otwarte
Wyznacz największą liczbę całkowitą spełniającą nierówność: 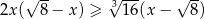 .
.
Rozwiąż równanie 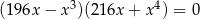 .
.
Wykaż, że jeżeli 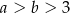 , to
, to 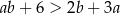 .
.
Doświadczenie losowe polega na trzykrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymamy sumę oczek równą 17.
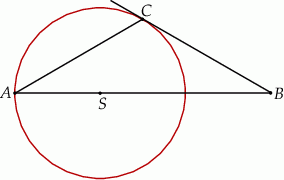
Wierzchołki 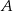 i
i 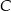 trójkąta
trójkąta 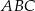 leżą na okręgu o promieniu
leżą na okręgu o promieniu  , a środek
, a środek 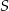 tego okręgu leży na boku
tego okręgu leży na boku 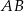 trójkąta (zobacz rysunek). Prosta
trójkąta (zobacz rysunek). Prosta 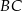 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 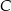 , a ponadto
, a ponadto 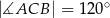 . Wykaż, że
. Wykaż, że 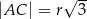 .
.
Prosta 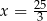 jest osią symetrii paraboli będącej wykresem funkcji kwadratowej
jest osią symetrii paraboli będącej wykresem funkcji kwadratowej 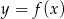 . Do wykresu tego należy punkt o współrzędnych
. Do wykresu tego należy punkt o współrzędnych 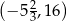 . Wyznacz wszystkie rozwiązania równania
. Wyznacz wszystkie rozwiązania równania 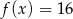 .
.
Ciąg arytmetyczny 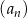 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 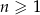 . Różnicą tego ciągu jest liczba
. Różnicą tego ciągu jest liczba 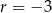 , a średnia arytmetyczna początkowych siedmiu wyrazów tego ciągu:
, a średnia arytmetyczna początkowych siedmiu wyrazów tego ciągu: 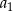 ,
, 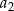 ,
, 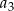 ,
, 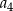 ,
, 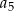 ,
, 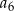 ,
, 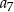 , jest równa
, jest równa 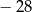 .
.
- Oblicz pierwszy wyraz tego ciągu.
- Wyznacz najmniejszą liczbę
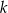 , dla której
, dla której 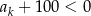 .
.
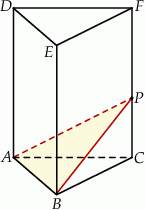
Dany jest graniastosłup prawidłowy trójkątny 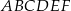 o podstawach
o podstawach 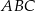 i
i 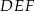 i krawędziach bocznych
i krawędziach bocznych 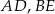 i
i 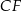 (zobacz rysunek). Przez krawędź
(zobacz rysunek). Przez krawędź 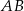 poprowadzono płaszczyznę nachyloną do płaszczyzny podstawy pod kątem
poprowadzono płaszczyznę nachyloną do płaszczyzny podstawy pod kątem 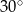 . Płaszczyzna ta przecina krawędź
. Płaszczyzna ta przecina krawędź 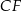 w punkcie
w punkcie 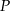 . Oblicz pole trójkąta
. Oblicz pole trójkąta 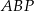 jeżeli objętość ostrosłupa
jeżeli objętość ostrosłupa 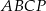 jest równa
jest równa 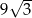 .
.
Oblicz pole ośmiokąta foremnego wpisanego w okrąg o promieniu 6.

