/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 3 marca 2018 Czas pracy: 180 minut
Zadania zamknięte
Liczba rozwiązań równania 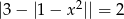 jest równa
jest równa
A) 6 B) 4 C) 2 D) 5
Liczba 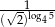 jest równa
jest równa
A) 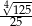 B)
B) 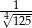 C)
C) 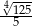 D)
D) 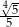
Bok 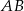 trójkąta
trójkąta 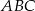 jest średnicą okręgu o środku
jest średnicą okręgu o środku 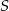 , a boki
, a boki 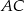 i
i 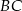 przecinają ten okrąg odpowiednio w punktach
przecinają ten okrąg odpowiednio w punktach 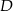 i
i 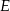 (zobacz rysunek). Ponadto
(zobacz rysunek). Ponadto 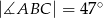 i
i 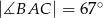 .
.
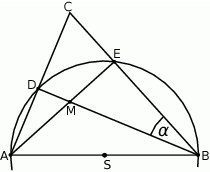
Zaznaczony na rysunku kąt  jest równy
jest równy
A) 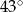 B)
B) 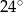 C)
C) 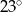 D)
D) 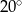
Ile jest liczb naturalnych sześciocyfrowych, których iloczyn cyfr jest różny od 49?
A) 899 970 B) 899 969 C) 899 985 D) 899 984
Na rysunku przedstawiono fragment wykresu pochodnej 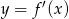 funkcji
funkcji 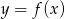 .
.
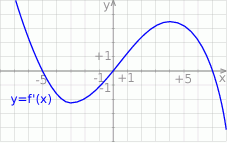
Wynika stąd, że
A) 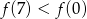 B)
B) 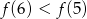 C)
C) 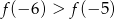 D)
D) 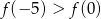
Zadania otwarte
Oblicz sumę szeregu
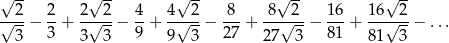
Napisz równanie stycznej do wykresu funkcji 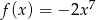 w punkcie
w punkcie 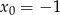 .
.
Doświadczenie losowe polega na tym, że losujemy jednocześnie dwie liczby ze zbioru
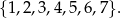
Oblicz prawdopodobieństwo warunkowe, że wśród wylosowanych liczb jest liczba 6, pod warunkiem, że suma wylosowanych liczb jest parzysta.
Oblicz granicę jednostronną funkcji 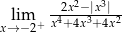 .
.
W trójkącie 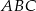 bok
bok 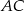 ma długość
ma długość 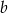 ,
, 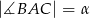 oraz
oraz 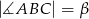 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 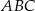 jest równe
jest równe
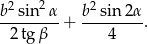
Dany jest graniastosłup prawidłowy trójkątny 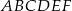 o podstawach
o podstawach 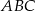 i
i 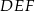 , w którym wszystkie krawędzie mają tę samą długość. Wykaż, że jeżeli przekrój tego graniastosłupa płaszczyzną zawierającą krawędź podstawy
, w którym wszystkie krawędzie mają tę samą długość. Wykaż, że jeżeli przekrój tego graniastosłupa płaszczyzną zawierającą krawędź podstawy 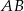 jest trapezem, to płaszczyzna ta jest nachylona do płaszczyzny podstawy
jest trapezem, to płaszczyzna ta jest nachylona do płaszczyzny podstawy 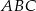 tego graniastosłupa pod takim kątem
tego graniastosłupa pod takim kątem  , że
, że 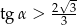 .
.
Funkcja 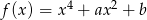 przyjmuje wartość 1 dla czterech argumentów:
przyjmuje wartość 1 dla czterech argumentów:
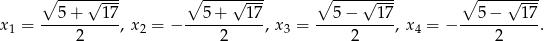
Oblicz najmniejszą wartość tej funkcji.
Oblicz sumę długości środkowych trójkąta o długościach boków: 2, 3 i 4.
Ciąg 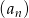 jest geometryczny, a ciąg
jest geometryczny, a ciąg 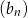 jest arytmetyczny. Pierwszy wyraz
jest arytmetyczny. Pierwszy wyraz 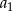 ciągu geometrycznego jest różnicą ciągu arytmetycznego
ciągu geometrycznego jest różnicą ciągu arytmetycznego 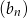 . Wyrazy ciągu
. Wyrazy ciągu 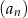 są liczbami całkowitymi, a suma dwóch początkowych wyrazów tego ciągu jest równa 28. Natomiast pierwszy wyraz
są liczbami całkowitymi, a suma dwóch początkowych wyrazów tego ciągu jest równa 28. Natomiast pierwszy wyraz 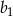 ciągu arytmetycznego jest ilorazem ciągu geometrycznego
ciągu arytmetycznego jest ilorazem ciągu geometrycznego 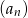 . Suma siedmiu pierwszych wyrazów ciągu arytmetycznego
. Suma siedmiu pierwszych wyrazów ciągu arytmetycznego 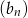 jest równa 126. Wyznacz te ciągi.
jest równa 126. Wyznacz te ciągi.
Wyznacz wszystkie wartości parametru 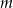 , dla których równanie
, dla których równanie
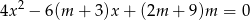
ma dwa różne rozwiązania rzeczywiste 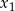 i
i 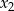 , przy czym
, przy czym 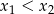 , spełniające warunek
, spełniające warunek
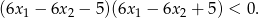
Wyznacz równanie okręgu stycznego wewnętrznie do okręgu o równaniu 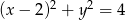 i do prostej
i do prostej 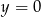 , którego środek ma współrzędne różnych znaków i leży na wykresie funkcji
, którego środek ma współrzędne różnych znaków i leży na wykresie funkcji 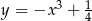 .
.
Rozpatrujemy wszystkie stożki o tworzącej długości 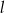 . Oblicz wysokość i promień podstawy tego stożka, którego objętość jest największa. Oblicz tę największą objętość.
. Oblicz wysokość i promień podstawy tego stożka, którego objętość jest największa. Oblicz tę największą objętość.

