/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 5 marca 2022 Czas pracy: 170 minut
Zadania zamknięte
Wartość wyrażenia 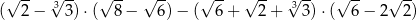 jest równa
jest równa
A) 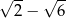 B) 2 C)
B) 2 C) 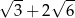 D)
D) 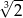
Funkcja wykładnicza określona wzorem 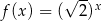 przyjmuje wartość 3 dla argumentu
przyjmuje wartość 3 dla argumentu
A) 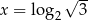 B)
B) 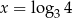 C)
C) 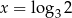 D)
D) 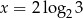
Liczba  stanowi 125% liczby dodatniej
stanowi 125% liczby dodatniej 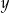 . Wynika stąd, że liczba
. Wynika stąd, że liczba 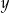 to
to
A) 125% liczby  B) 75% liczby
B) 75% liczby  C) 25% liczby
C) 25% liczby  D) 80% liczby
D) 80% liczby 
Suma 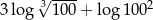 jest równa
jest równa
A) 6 B) 3 C) 4 D) 5
Liczbą niewymierną jest liczba
A) 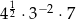 B)
B) 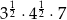 C)
C) 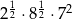 D)
D) 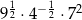
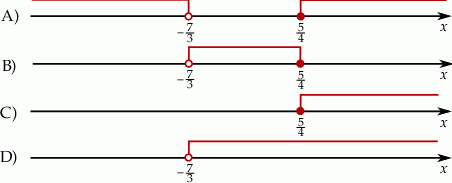
Wskaż rysunek, na którym przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających jednocześnie nierówności 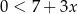 oraz
oraz 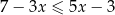 .
.
Gdy przesuniemy wykres funkcji 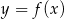 o 2 jednostki w lewo i o 3 jednostki w dół, to otrzymamy wykres funkcji
o 2 jednostki w lewo i o 3 jednostki w dół, to otrzymamy wykres funkcji 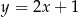 . Zatem
. Zatem
A) 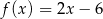 B)
B) 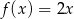 C)
C) 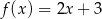 D)
D) 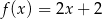
Na rysunku przedstawiono fragmenty dwóch prostych na płaszczyźnie oraz zaznaczono kilka punktów o współrzędnych całkowitych, przez które przechodzą te proste.
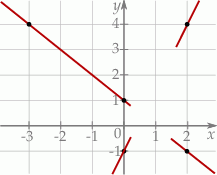
Jeżeli 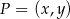 jest punktem wspólnym prostych, których fragmenty przedstawiono na rysunku, to
jest punktem wspólnym prostych, których fragmenty przedstawiono na rysunku, to
A) 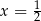 B)
B) 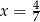 C)
C) 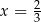 D)
D) 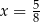
Na rysunku przedstawiono wykres funkcji 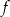 określonej w zbiorze
określonej w zbiorze 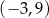 .
.
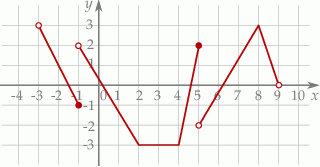
Wskaż zdanie prawdziwe.
A) Zbiorem wartości funkcji 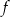 jest przedział
jest przedział 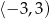
B) Funkcje 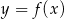 i
i 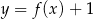 mają tyle samo miejsc zerowych
mają tyle samo miejsc zerowych
C) Funkcja 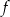 osiąga wartość równą 2 w trzech punktach.
osiąga wartość równą 2 w trzech punktach.
D) Wartość funkcji 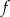 dla argumentu
dla argumentu 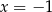 jest liczbą dodatnią.
jest liczbą dodatnią.
Zdanie „kwadrat różnicy dwóch kolejnych liczb naturalnych nieparzystych jest niemniejszy niż 5” można zapisać w postaci nierówności:
A) ![2 [(n + 3) − (n + 2)] ≥ 5](https://img.zadania.info/zes/0066767/HzesT46x.gif) B)
B) 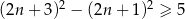
C) 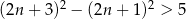 D)
D) ![[(2n + 3) − (2n + 1 )]2 ≥ 5](https://img.zadania.info/zes/0066767/HzesT49x.gif)
Funkcja 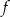 jest określona wzorem
jest określona wzorem 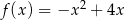 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Zbiorem wartości funkcji
. Zbiorem wartości funkcji 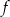 jest przedział
jest przedział
A) 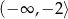 B)
B) 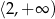 C)
C) 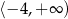 D)
D) 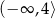
Funkcja kwadratowa 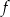 określona wzorem
określona wzorem 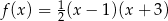 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 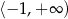 B)
B) 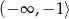 C)
C) 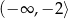 D)
D) 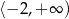
Liczba rozwiązań równania 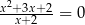 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Suma wszystkich trzycyfrowych liczb parzystych jest równa
A) 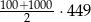 B)
B) 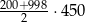 C)
C) 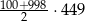 D)
D) 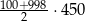
Ciąg geometryczny 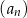 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 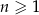 , jest rosnący i wszystkie jego wyrazy są dodatnie. Ponadto spełniony jest warunek
, jest rosnący i wszystkie jego wyrazy są dodatnie. Ponadto spełniony jest warunek 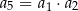 . Niech
. Niech 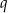 oznacza iloraz ciągu
oznacza iloraz ciągu 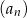 . Wtedy
. Wtedy
A) 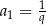 B)
B) 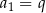 C)
C) 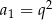 D)
D) 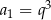
Wyrażenie 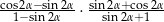 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 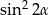 B)
B) 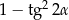 C)
C) 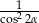 D)
D) 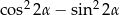
Dany jest ciąg geometryczny 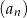 o wszystkich wyrazach niezerowych i pierwszym wyrazie
o wszystkich wyrazach niezerowych i pierwszym wyrazie 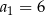 . Jeżeli
. Jeżeli 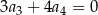 , to wzorem ogólnym ciągu
, to wzorem ogólnym ciągu 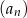 jest
jest
A) 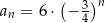 B)
B) 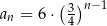 C)
C) 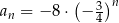 D)
D) 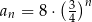
Bok rombu ma długość równą 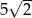 . Przekątne tego rombu nie mogą mieć długości
. Przekątne tego rombu nie mogą mieć długości
A) 14 i 2 B) 10 i 10 C) 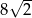 i
i 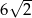 D)
D) 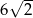 i
i 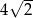
Punkty 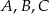 i
i 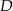 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 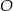 . Cięciwy
. Cięciwy 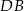 i
i 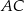 przecinają się w punkcie
przecinają się w punkcie 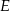 ,
, 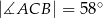 oraz
oraz 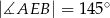 (zobacz rysunek).
(zobacz rysunek).
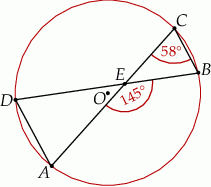
Miara kąta 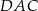 jest równa
jest równa
A) 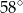 B)
B) 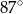 C)
C) 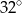 D)
D) 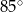
W trójkącie 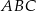 bok
bok 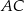 ma długość 10, a wysokość
ma długość 10, a wysokość 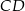 tego trójkąta dzieli bok
tego trójkąta dzieli bok 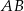 na odcinki o długościach
na odcinki o długościach 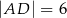 i
i 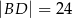 (zobacz rysunek obok).
(zobacz rysunek obok).
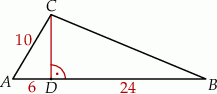
Długość boku 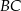 jest równa
jest równa
A) 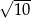 B)
B) 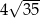 C)
C) 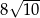 D)
D) 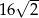
Dany jest odcinek 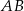 , gdzie
, gdzie 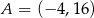 i
i 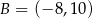 oraz prosta
oraz prosta 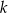 o równaniu
o równaniu 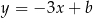 . Jeżeli prosta
. Jeżeli prosta 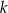 przecina odcinek
przecina odcinek 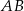 w takim punkcie
w takim punkcie 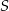 , że
, że 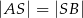 , to liczba
, to liczba 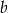 jest równa
jest równa
A) 31 B) 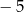 C) 4 D)
C) 4 D) 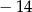
Proste o równaniach 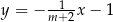 i
i 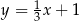 są równoległe. Wynika stąd, że
są równoległe. Wynika stąd, że
A) 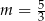 B)
B) 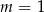 C)
C) 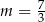 D)
D) 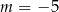
Punkt 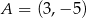 jest wierzchołkiem sześciokąta foremnego
jest wierzchołkiem sześciokąta foremnego 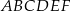 wpisanego w okrąg o środku
wpisanego w okrąg o środku 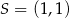 . Pole tego sześciokąta jest równe
. Pole tego sześciokąta jest równe
A) 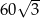 B)
B) 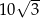 C)
C) 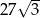 D)
D) 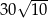
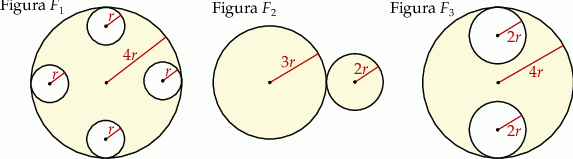
Na rysunku przedstawiono trzy figury. Figura 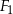 powstała z koła o promieniu
powstała z koła o promieniu 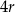 , z którego wycięto wnętrza czterech kół o promieniu
, z którego wycięto wnętrza czterech kół o promieniu  . Figura
. Figura 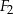 składa się z dwóch stycznych zewnętrznie kół o promieniach
składa się z dwóch stycznych zewnętrznie kół o promieniach 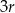 i
i 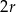 . Figura
. Figura 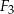 powstała z koła o promieniu
powstała z koła o promieniu 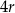 , z którego wycięto wnętrza dwóch kół o promieniu
, z którego wycięto wnętrza dwóch kół o promieniu 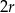 .
.
Jeżeli 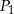 ,
, 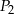 i
i 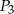 oznaczają pola figur odpowiednio
oznaczają pola figur odpowiednio 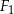 ,
, 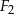 i
i 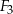 , to
, to
A) 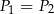 i
i 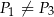 B)
B) 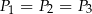
C) 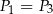 i
i 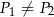 D)
D) 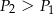
Łukasz dodał do siebie liczby krawędzi, wierzchołków oraz ścian pewnego graniastosłupa. Którą z liczb mógł otrzymać w wyniku?
A) 103 B) 104 C) 105 D) 106
Ile jest wszystkich czterocyfrowych liczb naturalnych podzielnych przez 13?
A) 692 B) 691 C) 690 D) 693
W pudełku znajdują się tylko kule białe i kule czerwone. Stosunek liczby kul białych do liczby kul czerwonych jest równy 4:5. Wylosowanie każdej kuli z tego pudełka jest jednakowo prawdopodobne. Losujemy jedną kulę. Niech 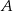 oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia 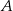 jest równe
jest równe
A) 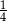 B)
B) 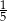 C)
C) 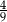 D)
D) 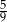
Sześciowyrazowy ciąg liczbowy 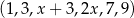 jest niemalejący. Mediana wyrazów tego ciągu jest równa 6. Wynika stąd, że
jest niemalejący. Mediana wyrazów tego ciągu jest równa 6. Wynika stąd, że
A) 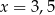 B)
B) 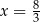 C)
C) 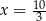 D)
D) 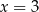
Zadania otwarte
Rozwiąż równanie: 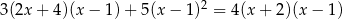 .
.
W graniastosłupie prawidłowym trójkątnym powierzchnia boczna po rozwinięciu jest kwadratem o polu 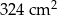 . Oblicz objętość tej bryły .
. Oblicz objętość tej bryły .
Wykaż, że dla dowolnej liczby całkowitej 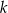 prawdziwa jest nierówność
prawdziwa jest nierówność 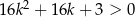 .
.
Rozwiąż równanie
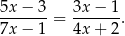
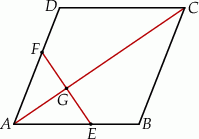
Na bokach 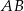 i
i 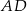 rombu
rombu 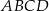 wybrano odpowiednio punkty
wybrano odpowiednio punkty 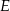 i
i 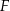 tak, że
tak, że 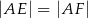 . Pole pięciokąta
. Pole pięciokąta 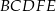 jest 17 razy większe niż pole trójkąta
jest 17 razy większe niż pole trójkąta 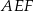 . Punkt
. Punkt 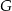 jest punktem wspólnym odcinka
jest punktem wspólnym odcinka 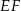 i przekątnej
i przekątnej 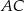 . Oblicz Oblicz
. Oblicz Oblicz 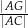 .
.
Punkty 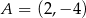 ,
, 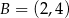 i
i 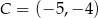 są wierzchołkami trójkąta
są wierzchołkami trójkąta 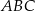 . Napisz równanie prostej zawierającej tą średnicę okręgu opisanego na trójkącie
. Napisz równanie prostej zawierającej tą średnicę okręgu opisanego na trójkącie 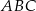 , której końcem jest punkt
, której końcem jest punkt 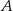 .
.
Dany jest ciąg 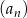 określony wzorem
określony wzorem 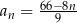 dla każdej liczby naturalnej
dla każdej liczby naturalnej 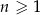 . Trójwyrazowy ciąg
. Trójwyrazowy ciąg 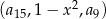 , gdzie
, gdzie  jest dodatnią liczbą rzeczywistą, jest geometryczny. Oblicz
jest dodatnią liczbą rzeczywistą, jest geometryczny. Oblicz  oraz iloraz tego ciągu geometrycznego.
oraz iloraz tego ciągu geometrycznego.

