/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 27 marca 2021 Czas pracy: 180 minut
Zadania zamknięte
Liczba 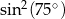 jest równa
jest równa
A) 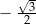 B)
B) 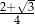 C)
C) 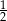 D)
D) 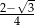
Prosta o równaniu 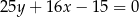 jest prostopadła do stycznej do wykresu funkcji
jest prostopadła do stycznej do wykresu funkcji 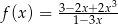 w punkcie
w punkcie
A) 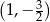 B)
B) 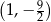 C)
C) 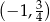 D)
D) 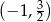
Dane są dwie urny z kulami. W pierwszej urnie jest 10 kul: 8 białych i 2 czarne, w drugiej jest 8 kul: 5 białych i 3 czarne. Wylosowanie każdej z urn jest jednakowo prawdopodobne. Wylosowano jedną z tych urn i wyciągnięto z niej losowo jedną kulę. Wyciągnięta kula była biała. Prawdopodobieństwo zdarzenia, że wylosowana kula pochodziła z drugiej z tych urn, jest równe
A) 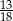 B)
B) 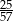 C)
C) 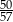 D)
D) 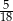
Po przekształceniu wyrażenia algebraicznego 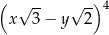 do postaci
do postaci 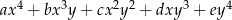 współczynnik
współczynnik  jest równy
jest równy
A) 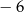 B)
B) 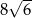 C) 36 D)
C) 36 D) 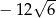
Zadania otwarte
Dane są takie liczby dodatnie  i
i 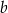 , że ciąg
, że ciąg 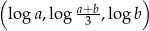 jest ciągiem arytmetycznym. Oblicz wartość wyrażenia
jest ciągiem arytmetycznym. Oblicz wartość wyrażenia 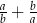 .
.
Przekątne czworokąta wypukłego 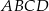 dzielą go na cztery trójkąty. Wykaż, że jeżeli promienie okręgów opisanych na tych czterech trójkątach są równe, to w czworokąt
dzielą go na cztery trójkąty. Wykaż, że jeżeli promienie okręgów opisanych na tych czterech trójkątach są równe, to w czworokąt 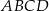 można wpisać okrąg.
można wpisać okrąg.
Liczby rzeczywiste  i
i 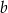 spełniają równość
spełniają równość 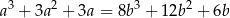 . Wykaż, że
. Wykaż, że 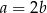 .
.
Wyznacz zbiór wartości funkcji
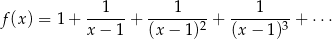
określonej dla wszystkich wartości  , dla których prawa strona powyższego wzoru jest sumą wyrazów zbieżnego szeregu geometrycznego.
, dla których prawa strona powyższego wzoru jest sumą wyrazów zbieżnego szeregu geometrycznego.
Dany jest trapez 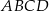 o podstawach
o podstawach 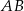 i
i 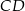 , w którym
, w którym 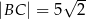 . Okrąg opisany na trójkącie
. Okrąg opisany na trójkącie 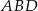 przecina prostą
przecina prostą 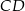 w takim punkcie
w takim punkcie 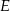 , że
, że 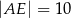 i
i 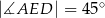 . Oblicz długość podstawy
. Oblicz długość podstawy 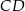 trapezu
trapezu 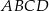 .
.
Rozwiąż równanie
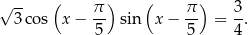
Sześcian 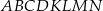 przecięto płaszczyzną przechodzącą przez przekątną
przecięto płaszczyzną przechodzącą przez przekątną 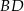 podstawy, która jest nachylona do płaszczyzny podstawy pod kątem
podstawy, która jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 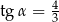 (zobacz rysunek).
(zobacz rysunek).
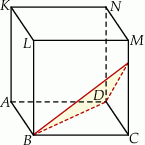
Odległość wierzchołka 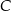 od płaszczyzny tego przekroju jest równa 6. Oblicz objętość sześcianu
od płaszczyzny tego przekroju jest równa 6. Oblicz objętość sześcianu 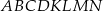 .
.
Wyznacz wszystkie wartości parametru 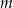 , dla których oba pierwiastki równania
, dla których oba pierwiastki równania
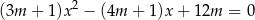
są większe od 2.
Punkt 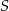 jest punktem przecięcia się środkowych trójkąta równoramiennego
jest punktem przecięcia się środkowych trójkąta równoramiennego 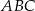 o podstawie
o podstawie 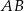 . Okrąg o średnicy
. Okrąg o średnicy 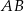 ma równanie
ma równanie 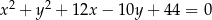 , a cięciwa tego okręgu równoległa do prostej
, a cięciwa tego okręgu równoległa do prostej 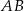 i przechodząca przez punkt
i przechodząca przez punkt 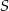 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 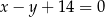 . Wyznacz równanie okręgu o środku
. Wyznacz równanie okręgu o środku 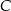 , który przechodzi przez punkty
, który przechodzi przez punkty 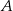 i
i 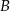 .
.
Ze zbioru liczb 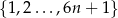 ,
, 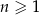 losujemy kolejno trzy razy po jednej liczbie bez zwracania. Niech
losujemy kolejno trzy razy po jednej liczbie bez zwracania. Niech 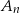 oznacza zdarzenie polegające na tym, że iloczyn wylosowanych liczb jest podzielny przez 6. Oblicz granicę
oznacza zdarzenie polegające na tym, że iloczyn wylosowanych liczb jest podzielny przez 6. Oblicz granicę 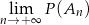 .
.
Rozpatrujemy wszystkie trapezy 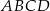 , których wierzchołki
, których wierzchołki 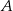 i
i 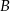 leżą na wykresie funkcji
leżą na wykresie funkcji 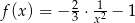 określonej dla
określonej dla 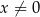 . Punkt
. Punkt 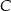 ma współrzędne
ma współrzędne 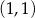 , a oś
, a oś 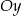 jest osią symetrii tego trapezu (zobacz rysunek).
jest osią symetrii tego trapezu (zobacz rysunek).
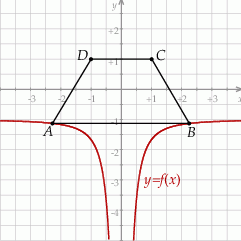
Oblicz obwód tego trapezu  , którego pole jest najmniejsze możliwe.
, którego pole jest najmniejsze możliwe.

