/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 25 marca 2017 Czas pracy: 170 minut
Zadania zamknięte
Najmniejszą liczbą całkowitą spełniającą nierówność 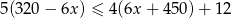 jest
jest
A) 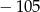 B)
B) 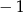 C)
C) 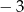 D)
D) 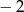
Liczba 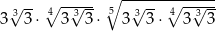 jest równa
jest równa
A) 9 B) 3 C) 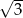 D)
D) 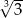
Liczby  i
i  są dodatnie. Liczba
są dodatnie. Liczba 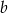 stanowi 42% liczby
stanowi 42% liczby  oraz 56% liczby
oraz 56% liczby  . Wynika stąd, że
. Wynika stąd, że
A) 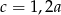 B)
B) 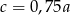 C)
C) 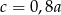 D)
D) 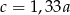
Liczba 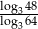 jest równa
jest równa
A) 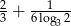 B)
B) 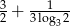 C)
C) 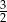 D)
D) 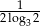
Najmniejsza wartość wyrażenia 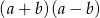 dla
dla 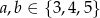 jest równa
jest równa
A) 2 B) 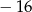 C) 0 D)
C) 0 D) 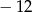
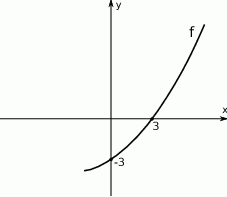
Na rysunku obok jest przedstawiony fragment wykresu funkcji kwadratowej 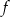 . Osią symetrii paraboli jest prosta o równaniu
. Osią symetrii paraboli jest prosta o równaniu 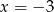 .
.
Rozwiązaniem nierówności 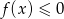 jest zbiór
jest zbiór
A) 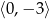 B)
B) 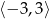 C)
C) 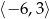 D)
D) 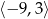
Punkty 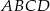 leżą na okręgu o środku
leżą na okręgu o środku 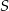 (zobacz rysunek). Miara kąta
(zobacz rysunek). Miara kąta 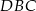 jest równa
jest równa
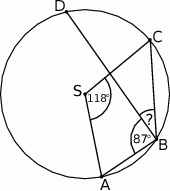
A) 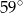 B)
B)  C)
C) 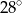 D)
D) 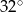
Rozwiązaniem równania 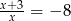 , gdzie
, gdzie 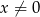 , jest liczba należąca do przedziału
, jest liczba należąca do przedziału
A) 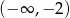 B)
B) 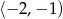 C)
C) 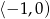 D)
D) 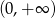
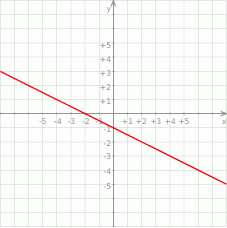
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej 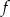 , przy czym
, przy czym 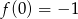 i
i 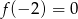 .
.
Wykres funkcji 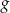 jest symetryczny do wykresu funkcji
jest symetryczny do wykresu funkcji 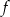 względem początku układu współrzędnych. Funkcja
względem początku układu współrzędnych. Funkcja 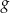 jest określona wzorem
jest określona wzorem
A) 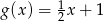 B)
B) 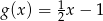 C)
C) 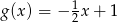 D)
D) 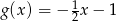
Jeśli wykres funkcji kwadratowej 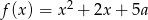 przecina prostą
przecina prostą 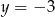 , to liczba
, to liczba  spełnia warunek
spełnia warunek
A) 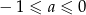 B)
B) 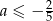 C)
C) 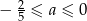 D)
D) 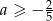
Układ równań 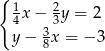
A) nie ma rozwiązań.
B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania.
D) ma nieskończenie wiele rozwiązań.
Funkcja 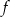 określona jest wzorem
określona jest wzorem 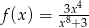 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wtedy liczba
. Wtedy liczba 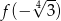 jest równa
jest równa
A) 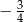 B)
B) 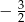 C)
C) 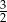 D)
D) 
Ciąg 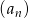 jest określony wzorem
jest określony wzorem 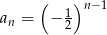 dla
dla 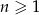 . Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
A) 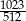 B)
B) 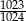 C)
C) 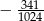 D)
D) 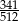
Wartość wyrażenia 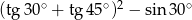 jest równa
jest równa
A) 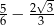 B)
B) 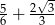 C)
C) 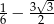 D)
D) 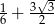
Powierzchnia boczna walca o objętości 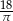 po rozwinięciu jest prostokątem, w którym przekątna tworzy z wysokością walca kąt o mierze
po rozwinięciu jest prostokątem, w którym przekątna tworzy z wysokością walca kąt o mierze 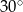 . Promień podstawy tego walca jest równy
. Promień podstawy tego walca jest równy
A) 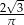 B)
B) 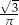 C)
C) 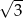 D)
D) 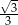
Odległości punktu 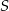 przecięcia przekątnych czworokąta przedstawionego na rysunku od wierzchołków
przecięcia przekątnych czworokąta przedstawionego na rysunku od wierzchołków 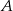 i
i 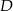 są równe
są równe 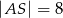 i
i 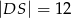 . Bok
. Bok 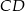 tego czworokąta ma długość
tego czworokąta ma długość
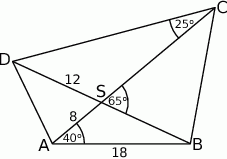
A) 27 B) 16 C) 24 D) 30
Każde z ramion trójkąta równoramiennego ma długość 20. Kąt zawarty między ramionami tego trójkąta ma miarę 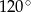 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 100 B) 200 C) 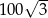 D)
D) 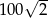
Wykonano pomiary wysokości czterech krzeseł i każde dwa rezultaty były różne. Adam zapisał wyniki w metrach i odchylenie standardowe jego danych było równe 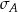 . Bogdan zapisał te same wyniki w centymetrach i odchylenie standardowe jego danych było równe
. Bogdan zapisał te same wyniki w centymetrach i odchylenie standardowe jego danych było równe 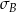 . Wynika stąd, że
. Wynika stąd, że
A) 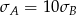 B)
B) 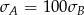 C)
C) 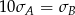 D)
D) 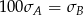
Ile jest wszystkich dwucyfrowych liczb naturalnych podzielnych przez 4?
A) 21 B) 22 C) 23 D) 24
Proste opisane równaniami 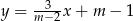 oraz
oraz 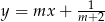 są prostopadłe, gdy
są prostopadłe, gdy
A) 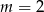 B)
B) 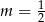 C)
C) 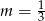 D)
D) 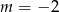
Z talii 52 kart losujemy dwa razy po jednej karcie (ze zwracaniem). Niech 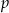 oznacza prawdopodobieństwo wylosowania dwóch królów. Wtedy
oznacza prawdopodobieństwo wylosowania dwóch królów. Wtedy
A) 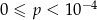 B)
B) 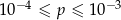 C)
C) 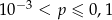 D)
D) 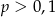
Okręgi o środkach 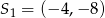 oraz
oraz 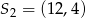 są styczne wewnętrznie. Promień pierwszego z tych okręgów jest 6 razy większy od promienia drugiego okręgu. Suma promieni tych okręgów jest równa
są styczne wewnętrznie. Promień pierwszego z tych okręgów jest 6 razy większy od promienia drugiego okręgu. Suma promieni tych okręgów jest równa
A) 28 B) 24 C) 20 D) 16
Liczb naturalnych trzycyfrowych, w zapisie których każda cyfra występuje co najwyżej raz oraz suma cyfry setek i cyfry jedności jest równa 4, jest
A) mniej niż 24 B) dokładnie 24 C) dokładnie 32 D) więcej niż 32
Przekątna podstawy graniastosłupa prawidłowego czworokątnego ma długość 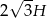 , gdzie
, gdzie 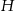 jest wysokością tego graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
jest wysokością tego graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
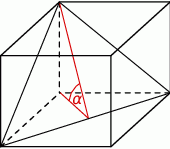
Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt  o mierze
o mierze
A) 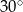 B)
B) 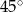 C)
C) 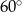 D)
D) 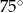
Zadania otwarte
Punkty 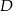 i
i 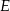 są takimi punktami przeciwprostokątnej
są takimi punktami przeciwprostokątnej 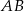 trójkąta prostokątnego
trójkąta prostokątnego 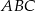 , że
, że 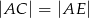 i
i 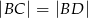 . Wykaż, że
. Wykaż, że 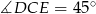 .
.
Rozwiąż równanie 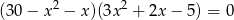 .
.
Wykaż, że dla dowolnych liczb rzeczywistych 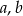 prawdziwa jest nierówność
prawdziwa jest nierówność
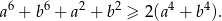
Dane są dwa podzbiory zbioru liczb całkowitych:
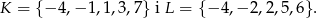
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest ujemny.
Skala Richtera służy do określania siły trzęsień ziemi. Siła ta opisana jest wzorem 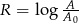 , gdzie
, gdzie 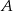 oznacza amplitudę trzęsienia wyrażoną w centymetrach,
oznacza amplitudę trzęsienia wyrażoną w centymetrach, 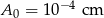 jest stałą, nazywaną amplitudą wzorcową. 27 lutego 2010 roku w Chile miało miejsce trzęsienie ziemi o sile 8,8 w skali Richtera. Oblicz amplitudę trzęsienia ziemi w Chile i rozstrzygnij, czy jest ona większa, czy – mniejsza od 100 m.
jest stałą, nazywaną amplitudą wzorcową. 27 lutego 2010 roku w Chile miało miejsce trzęsienie ziemi o sile 8,8 w skali Richtera. Oblicz amplitudę trzęsienia ziemi w Chile i rozstrzygnij, czy jest ona większa, czy – mniejsza od 100 m.
Wyznacz takie liczby  i
i 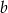 , dla których układ równań
, dla których układ równań 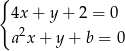 jest sprzeczny, zaś układ równań
jest sprzeczny, zaś układ równań 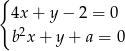 ma nieskończenie wiele rozwiązań.
ma nieskończenie wiele rozwiązań.
Dwudziestowyrazowy ciąg geometryczny 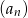 określony jest wzorem
określony jest wzorem 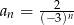 dla
dla 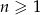 . Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
. Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
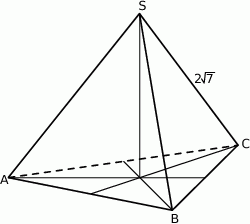
Trójkąt równoboczny 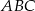 jest podstawą ostrosłupa prawidłowego
jest podstawą ostrosłupa prawidłowego 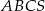 , w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem
, w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 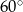 , a krawędź boczna ma długość
, a krawędź boczna ma długość 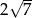 (zobacz rysunek). Oblicz objętość tego ostrosłupa.
(zobacz rysunek). Oblicz objętość tego ostrosłupa.
Punkt 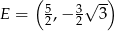 jest środkiem boku
jest środkiem boku 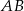 trójkąta równobocznego
trójkąta równobocznego 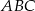 , a boki
, a boki 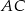 i
i 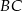 tego trójkąta są zawarte odpowiednio w prostych o równaniach
tego trójkąta są zawarte odpowiednio w prostych o równaniach 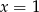 i
i 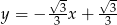 . Wyznacz współrzędne wierzchołków tego trójkąta.
. Wyznacz współrzędne wierzchołków tego trójkąta.

