/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 26 kwietnia 2008 Czas pracy: 180 minut
Narysuj wykres funkcji 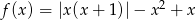 i odczytaj z niego ilość rozwiązań równania
i odczytaj z niego ilość rozwiązań równania 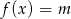 .
.
Punkty 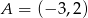 i
i 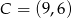 są przeciwległymi wierzchołkami rombu o polu 40. Wyznacz współrzędne pozostałych wierzchołków rombu.
są przeciwległymi wierzchołkami rombu o polu 40. Wyznacz współrzędne pozostałych wierzchołków rombu.
Fragment palisady wokół średniowiecznego grodu składa się z coraz krótszych pionowych bali. Najwyższy z bali ma długość 350 cm, a każdy kolejny jest krótszy o 5 cm. Wiedząc, że całkowita długość wszystkich bali wynosi 50 m oblicz ile jest tych bali i jaka jest długość najkrótszego z nich.
Oto w jaki sposób można uzasadnić, że suma odległości dowolnego punktu  wewnątrz trójkąta równobocznego od boków tego trójkąta jest stała, tzn. nie zależy od wyboru tego punktu.
wewnątrz trójkąta równobocznego od boków tego trójkąta jest stała, tzn. nie zależy od wyboru tego punktu.
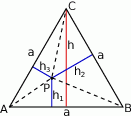
- Łączymy punkt
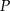 z wierzchołkami trójkąta i zapisujemy równość pól
z wierzchołkami trójkąta i zapisujemy równość pól 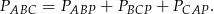
- Korzystamy ze wzoru na pole trójkąta
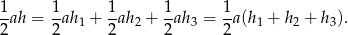
- Wnioskujemy, że
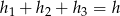 , a więc suma ta nie zależy od wyboru punktu
, a więc suma ta nie zależy od wyboru punktu 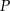 .
.
Postępując w analogiczny sposób wykaż, że suma odległości dowolnego punktu 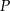 wewnątrz czworościanu foremnego od jego ścian jest stała, to znaczy nie zależy od wyboru punktu
wewnątrz czworościanu foremnego od jego ścian jest stała, to znaczy nie zależy od wyboru punktu 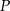 .
.
Dany jest ciąg geometryczny 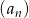 o pierwszym wyrazie równym
o pierwszym wyrazie równym 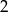 , i ilorazie równym 10. Wykaż, że wszystkie punkty o współrzędnych
, i ilorazie równym 10. Wykaż, że wszystkie punkty o współrzędnych 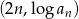 leżą na jednej prostej.
leżą na jednej prostej.
W ostrosłupie prawidłowym sześciokątnym pole przekroju płaszczyzną przechodzącą przez jego wysokość oraz przez dwie krawędzie boczne jest dwukrotnie większe od pola podstawy i wynosi 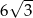 . Oblicz odległość spodka wysokości ostrosłupa od jego krawędzi bocznej.
. Oblicz odległość spodka wysokości ostrosłupa od jego krawędzi bocznej.
Wykres funkcji 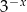 przesunięto o wektor
przesunięto o wektor ![→ v = [3,a]](https://img.zadania.info/zes/0081317/HzesT19x.gif) otrzymując wykres funkcji
otrzymując wykres funkcji 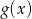 . Wiedząc, że wykresy funkcji
. Wiedząc, że wykresy funkcji 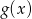 i
i 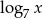 przecinają się na osi
przecinają się na osi 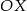 oblicz
oblicz  . Narysuj wykres funkcji
. Narysuj wykres funkcji 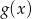 .
.
Liczbę naturalną nazywamy palindromiczną, jeżeli nie zmienia się po zapisaniu jej cyfr w odwrotnej kolejności. Liczbami palindromicznymi są np. liczby 5, 33, 1123211. Liczby 10, 3230 nie są palindromiczne.
- Oblicz prawdopodobieństwo, że losowo wybrana liczba siedmiocyfrowa jest liczbą palindromiczną.
- Oblicz prawdopodobieństwo, że suma dwóch losowo wybranych liczb dwucyfrowych jest nieparzystą dwucyfrową liczbą palindromiczną.
Liczby 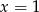 i
i 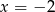 są pierwiastkami wielomianu
są pierwiastkami wielomianu 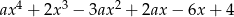 . Wiedząc, że wielomian ten jest kwadratem wielomianu stopnia 2, oblicz
. Wiedząc, że wielomian ten jest kwadratem wielomianu stopnia 2, oblicz  .
.
Dany jest pięciokąt foremny 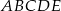 o boku długości
o boku długości  . Wiedząc, że
. Wiedząc, że 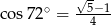
- wykaż, że długość przekątnej pięciokąta
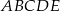 jest równa
jest równa 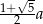 ;
; - oblicz długość promienia okręgu wpisanego w pięciokąt
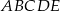 .
.
Wyznacz zbiór wartości funkcji 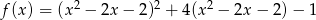 .
.

