/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 18 kwietnia 2015 Czas pracy: 180 minut
Zadania zamknięte
Wielomian 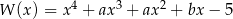 jest podzielny przez wielomian
jest podzielny przez wielomian 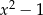 . Wynika stąd, że
. Wynika stąd, że
A) 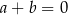 B)
B) 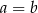 C)
C) 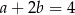 D)
D) 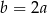
Liczba 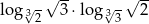 jest równa
jest równa
A) 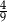 B)
B)  C)
C) 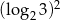 D)
D) 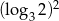
Funkcja 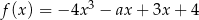 jest funkcją malejąca jeżeli
jest funkcją malejąca jeżeli
A) 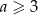 B)
B) 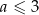 C)
C) 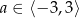 D)
D) 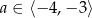
Wyrażenie 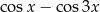 jest równe
jest równe
A) 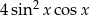 B)
B) 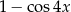 C)
C) 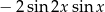 D)
D) 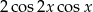
Funkcja 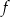 jest określona dla wszystkich liczb rzeczywistych wzorem
jest określona dla wszystkich liczb rzeczywistych wzorem 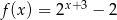 . Prosta
. Prosta 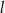 ma równanie
ma równanie 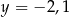 . Ile punktów wspólnych mają wykres funkcji
. Ile punktów wspólnych mają wykres funkcji 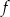 i prosta
i prosta 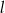 ?
?
A) Zero. B) Jeden. C) Dwa. D) Nieskończenie wiele.
Zadania otwarte
Wyznacz wszystkie wartości parametru 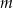 , dla których wśród rozwiązań równania
, dla których wśród rozwiązań równania
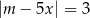
są zarówno liczby dodatnie, jak i ujemne.
Oblicz granicę 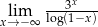 .
.
Funkcja 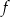 jest określona wzorem
jest określona wzorem 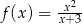 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 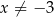 . Oblicz pochodną funkcji
. Oblicz pochodną funkcji 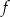 w punkcie
w punkcie 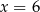 .
.
W loterii szkolnej losujemy jeden spośród 100 losów, przy czym w przypadku wyciągnięcia losu przegrywającego możemy wylosować jeszcze jeden los. Ile losów w tej loterii jest wygrywających, jeżeli prawdopodobieństwo wygranej jest równe 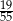 ?
?
Wykaż, że jeżeli 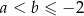 , to
, to 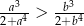 .
.
Uzasadnij, że jeżeli  i
i 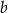 są liczbami całkowitymi i
są liczbami całkowitymi i 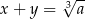 oraz
oraz 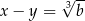 , to
, to 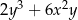 też jest liczbą całkowitą.
też jest liczbą całkowitą.
Dana jest parabola o równaniu 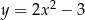 i leżący na niej punkt
i leżący na niej punkt 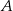 o współrzędnej
o współrzędnej  równej
równej 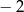 . Wyznacz równanie stycznej do tej paraboli w punkcie
. Wyznacz równanie stycznej do tej paraboli w punkcie 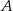 .
.
Monotoniczny ciąg geometryczny 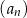 jest zdefiniowany przez warunki
jest zdefiniowany przez warunki
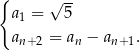
Oblicz sumę wszystkich wyrazów ciągu 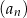 .
.
Wykaż, że
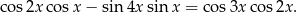
Oblicz jakie długości powinny mieć boki prostokąta o polu równym 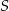 , aby jego przekątna miała najmniejszą możliwą długość. Oblicz długość tej przekątnej.
, aby jego przekątna miała najmniejszą możliwą długość. Oblicz długość tej przekątnej.
Rzucamy cztery razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma kwadratów liczb oczek otrzymanych we wszystkich czterech rzutach będzie mniejsza niż 20.
Punkt 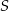 jest punktem przecięcia się przekątnych równoległoboku
jest punktem przecięcia się przekątnych równoległoboku 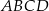 , a punkt
, a punkt 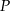 jest takim punktem boku
jest takim punktem boku 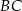 tego równoległoboku, że
tego równoległoboku, że 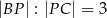 . Oblicz współrzędne spodka wysokości opuszczonej z wierzchołka
. Oblicz współrzędne spodka wysokości opuszczonej z wierzchołka 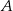 tego równoległoboku na prostą
tego równoległoboku na prostą 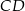 , jeżeli
, jeżeli ![−→ AB = [4,4]](https://img.zadania.info/zes/0081388/HzesT60x.gif) ,
, ![−→ DS = [3 ,− 3]](https://img.zadania.info/zes/0081388/HzesT61x.gif) i
i 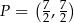 .
.
Oblicz promień kuli stycznej do wszystkich krawędzi czworościanu foremnego o krawędzi długości  .
.

