/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 14 kwietnia 2012 Czas pracy: 180 minut
Rozwiąż nierówność 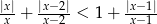 .
.
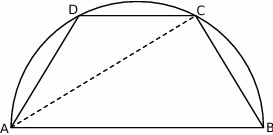
W półkole o promieniu  wpisano trapez równoramienny o krótszej podstawie długości
wpisano trapez równoramienny o krótszej podstawie długości  . Oblicz długość przekątnej trapezu.
. Oblicz długość przekątnej trapezu.
Uzasadnij, że dla każdej liczby dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność 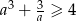 .
.
Długości boków 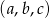 trójkąta tworzą ciąg geometryczny, przy czym kąt trójkąta leżący naprzeciwko boku długości
trójkąta tworzą ciąg geometryczny, przy czym kąt trójkąta leżący naprzeciwko boku długości 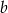 ma miarę
ma miarę 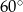 . Oblicz miary pozostałych kątów tego trójkąta.
. Oblicz miary pozostałych kątów tego trójkąta.
Wyznacz wszystkie wartości parametru 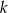 , dla których równanie
, dla których równanie 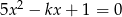 ma dwa różne pierwiastki, których różnica jest liczbą z przedziału
ma dwa różne pierwiastki, których różnica jest liczbą z przedziału 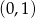 .
.
Wykaż, że jeżeli w czworokącie 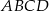 dwusieczne kątów przy wierzchołkach
dwusieczne kątów przy wierzchołkach  i
i  przecinają dwusieczne kątów przy wierzchołkach
przecinają dwusieczne kątów przy wierzchołkach 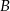 i
i 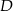 w czterech różnych punktach, to punkty te leżą na pewnym okręgu.
w czterech różnych punktach, to punkty te leżą na pewnym okręgu.
Punkt 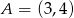 jest wierzchołkiem kąta prostego w równoramiennym trójkącie prostokątnym
jest wierzchołkiem kąta prostego w równoramiennym trójkącie prostokątnym 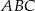 . Przeciwprostokątna tego trójkąta zawiera się w prostej o równaniu
. Przeciwprostokątna tego trójkąta zawiera się w prostej o równaniu 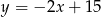 . Wyznacz współrzędne pozostałych wierzchołków trójkąta
. Wyznacz współrzędne pozostałych wierzchołków trójkąta 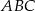 .
.
Wielomian 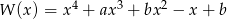 przy dzieleniu przez każdy z dwumianów:
przy dzieleniu przez każdy z dwumianów: 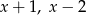 i
i 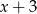 daję tę samą resztę. Wyznacz
daję tę samą resztę. Wyznacz  i
i 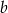 .
.
Udowodnij, że jeżeli 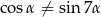 i
i 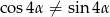 to
to
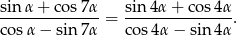
Listonosz losowo rozmieszcza 7 listów w 5 różnych skrzynkach na listy. Oblicz prawdopodobieństwo, że w każdej skrzynce znajdzie się przynajmniej jeden list.
Podstawą ostrosłupa prawidłowego trójkątnego  jest trójkąt
jest trójkąt  . Punkty
. Punkty  i
i 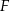 są rzutami punktów
są rzutami punktów 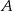 i
i 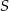 na przeciwległe ściany. Oblicz w jakim stosunku odcinek
na przeciwległe ściany. Oblicz w jakim stosunku odcinek 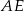 dzieli odcinek
dzieli odcinek 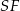 , jeżeli ściana boczna ostrosłupa jest nachylona do podstawy pod kątem, którego sinus jest równy
, jeżeli ściana boczna ostrosłupa jest nachylona do podstawy pod kątem, którego sinus jest równy  .
.

