/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 4 marca 2023 Czas pracy: 180 minut
Wartość wyrażenia 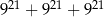 jest równa
jest równa
A) 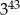 B)
B) 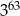 C)
C) 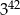 D)
D) 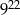
Cenę  pewnego towaru dwukrotnie obniżono o 20% i otrzymano cenę
pewnego towaru dwukrotnie obniżono o 20% i otrzymano cenę 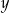 . Aby przywrócić cenę
. Aby przywrócić cenę  , nową cenę
, nową cenę 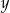 należy podnieść o
należy podnieść o
A) 40% B) 64% C) 75% D) 56,25%
Właściciel sklepu kupił w hurtowni 12 identycznych wiertarek po  zł za sztukę i 15 identycznych szlifierek kątowych po
zł za sztukę i 15 identycznych szlifierek kątowych po 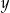 zł za sztukę. Za zakupy w hurtowni zapłacił 9120 zł. Po doliczeniu marży w wysokości 40 zł do każdej wiertarki i 25% na każdą szlifierkę kątową ceny detaliczne wiertarki i szlifierki były jednakowe. Cenę wiertarki
zł za sztukę. Za zakupy w hurtowni zapłacił 9120 zł. Po doliczeniu marży w wysokości 40 zł do każdej wiertarki i 25% na każdą szlifierkę kątową ceny detaliczne wiertarki i szlifierki były jednakowe. Cenę wiertarki  i szlifierki
i szlifierki 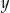 , jakie trzeba zapłacić w hurtowni, można obliczyć z układu równań
, jakie trzeba zapłacić w hurtowni, można obliczyć z układu równań
A) 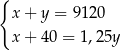 B)
B) 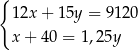
C) 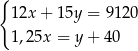 D)
D) 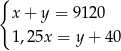
Ciąg 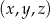 jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 27. Stąd wynika, że
jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 27. Stąd wynika, że 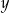 jest równe
jest równe
A) 81 B) 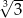 C) 9 D) 3
C) 9 D) 3
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Liczba 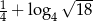 jest równa
jest równa
A) 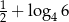 B)
B) 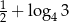 C)
C) 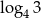
D) 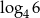 E)
E) 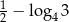 F)
F) 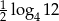
Dany jest wielomian 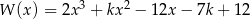 gdzie
gdzie 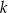 jest pewną liczbą rzeczywistą. Wiadomo, że liczba
jest pewną liczbą rzeczywistą. Wiadomo, że liczba 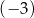 jest pierwiastkiem tego wielomianu. Liczba
jest pierwiastkiem tego wielomianu. Liczba 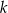 jest równa
jest równa
A) 2 B) 3 C) 6 D) 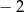
Dla każdej liczby rzeczywistej 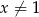 wyrażenie
wyrażenie 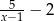 jest równe
jest równe
A) 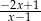 B)
B) 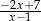 C)
C) 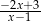 D)
D) 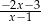
Informacja do zadań 8.1 – 8.3
Czas 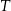 półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa
półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa 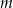 leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
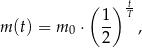
gdzie: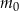 – masa przyjętej dawki leku
– masa przyjętej dawki leku 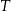 – czas półtrwania leku
– czas półtrwania leku 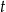 – czas liczony od momentu przyjęcia dawki.
– czas liczony od momentu przyjęcia dawki.
W przypadku przyjęcia kilku(nastu) dawek powyższa zależność pozwala obliczyć, ile leku pozostało w danym momencie w organizmie z każdej poprzednio przyjętej dawki. W ten sposób obliczone masy leku z przyjętych poprzednich dawek sumują się i dają informację o całkowitej aktualnej masie leku w organizmie.
Pan Karol otrzymuje codziennie o godz. 12:00 dawkę 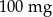 leku L. Pan Tomasz otrzymuje co 2 dni o godz. 12:00 dawkę
leku L. Pan Tomasz otrzymuje co 2 dni o godz. 12:00 dawkę 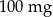 tego samego leku L. Pierwszą dawkę leku obaj panowie przyjęli tego samego dnia. Czas półtrwania tego leku w organizmie jest równy
tego samego leku L. Pierwszą dawkę leku obaj panowie przyjęli tego samego dnia. Czas półtrwania tego leku w organizmie jest równy 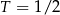 doby.
doby.
Wykres zależności masy 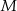 leku L w organizmie pana Karola od czasu
leku L w organizmie pana Karola od czasu 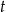 , liczonego od momentu przyjęcia przez niego pierwszej dawki, przedstawiono na rysunku
, liczonego od momentu przyjęcia przez niego pierwszej dawki, przedstawiono na rysunku
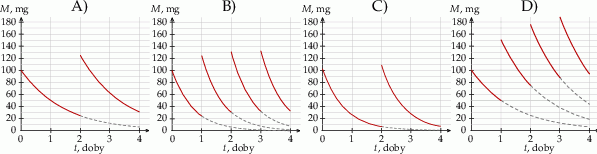
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Masa leku L w organizmie pana Tomasza tuż przed przyjęciem drugiej dawki jest dwa razy mniejsza niż masa tego leku dokładnie w tym samym czasie w organizmie pana Karola. | P | F |
| Masa leku L w organizmie pana Karola po 12 godzinach od przyjęcia pierwszej dawki zmniejszyła się o 50%. | P | F |
Oblicz masę leku L w organizmie pana Tomasza tuż przed przyjęciem szóstej dawki tego leku. Wynik podaj w zaokrągleniu do 0,01 mg.
Firma przeprowadziła badania rynkowe dotyczące wpływu zmiany ceny 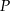 swojego produktu na liczbę
swojego produktu na liczbę 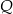 kupujących ten produkt. Z badań wynika, że każdorazowe zwiększenie ceny o 6 jednostek powoduje spadek liczby kupujących o 9 jednostek. Ponadto przy cenie równej 9 jednostek liczba kupujących jest równa 24 jednostki. Liczba kupujących ten produkt przy cenie równej 19 jednostek jest równa
kupujących ten produkt. Z badań wynika, że każdorazowe zwiększenie ceny o 6 jednostek powoduje spadek liczby kupujących o 9 jednostek. Ponadto przy cenie równej 9 jednostek liczba kupujących jest równa 24 jednostki. Liczba kupujących ten produkt przy cenie równej 19 jednostek jest równa
A) 10 jednostek B) 13 jednostek
C) 11 jednostek D) 9 jednostek
Równanie 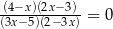 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie B) dwa rozwiązania
C) trzy rozwiązania D) cztery rozwiązania
Czterowyrazowy ciąg 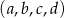 jest arytmetyczny i suma jego wyrazów jest równa 27. Suma
jest arytmetyczny i suma jego wyrazów jest równa 27. Suma 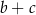 równa
równa
A) 27 B) 13,5 C) 17 D) 9
Informacja do zadań 12.1 i 12.2
W kartezjańskim układzie współrzędnych 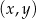 przedstawiono oś symetrii wykresu funkcji kwadratowej
przedstawiono oś symetrii wykresu funkcji kwadratowej 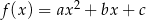 . Przedstawiono również prostą
. Przedstawiono również prostą 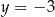 , z którą wykres funkcji
, z którą wykres funkcji 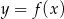 ma dokładnie jeden punkt wspólny, oraz jeden z punktów tego wykresu –
ma dokładnie jeden punkt wspólny, oraz jeden z punktów tego wykresu – 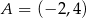
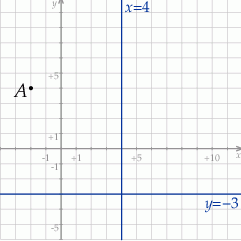
Wyznacz zbiór rozwiązań nierówności 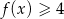 .
.
Wyznacz wzór funkcji kwadratowej 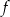 w postaci kanonicznej.
w postaci kanonicznej.
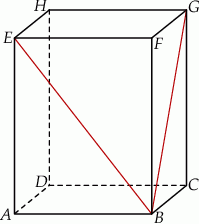
W prostopadłościanie 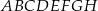 przekątna ściany
przekątna ściany 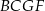 jest o 2 dłuższa od krawędzi
jest o 2 dłuższa od krawędzi 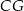 i o 4 dłuższa od krawędzi
i o 4 dłuższa od krawędzi 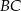 . Przekątna ściany
. Przekątna ściany 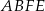 jest nachylona do płaszczyzny
jest nachylona do płaszczyzny 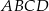 pod kątem
pod kątem 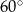 . Oblicz objętość tego prostopadłościanu.
. Oblicz objętość tego prostopadłościanu.
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 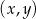 , dany jest okrąg o środku
, dany jest okrąg o środku 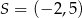 i promieniu
i promieniu 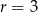 . Równanie tego okręgu ma postać
. Równanie tego okręgu ma postać
A) 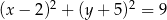 B)
B) 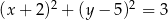
C) 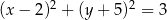 D)
D) 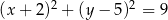
Oś 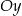 kartezjańskiego układu współrzędnych jest osią symetrii czworokąta
kartezjańskiego układu współrzędnych jest osią symetrii czworokąta 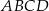 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Środek jednej z przekątnych czworokąta 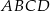 musi leżeć na osi musi leżeć na osi 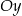 . . | P | F |
Czworokąt 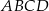 musi być trapezem. musi być trapezem. | P | F |
W trójkącie 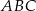 bok
bok 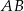 ma długość 8, a bok
ma długość 8, a bok 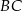 ma długość 10. Dwusieczna kąta
ma długość 10. Dwusieczna kąta 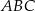 przecina bok
przecina bok 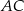 w punkcie
w punkcie 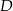 takim, że
takim, że 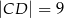 (zobacz rysunek).
(zobacz rysunek).
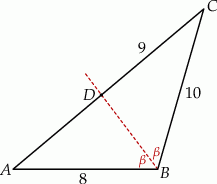
Oblicz długość odcinka 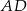 .
.
Punkty 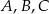 leżą na okręgu o środku
leżą na okręgu o środku 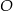 (zobacz rysunek). Ponadto
(zobacz rysunek). Ponadto 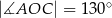 oraz
oraz 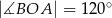 .
.
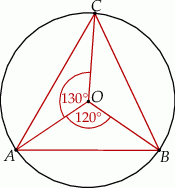
Miara kąta wewnętrznego 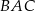 trójkąta
trójkąta 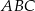 jest równa
jest równa
A) 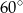 B)
B) 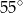 C)
C) 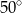 D)
D) 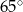
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 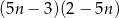 przy dzieleniu przez 25 daje resztę 19.
przy dzieleniu przez 25 daje resztę 19.
Ile można utworzyć liczb pięciocyfrowych podzielnych przez 20, w których zapisie dziesiętnym nie występuje cyfra 7?
A) 3645 B) 2592 C) 3240 D) 2560
Informacja do zadań 20.1 i 20.2
Bok 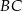 kwadratu
kwadratu 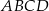 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 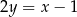 .
.
Bok 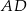 kwadratu
kwadratu 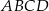 może zawierać się w prostej o równaniu
może zawierać się w prostej o równaniu
A) 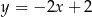 B)
B) 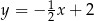 C)
C) 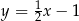 D)
D) 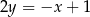
Bok 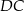 kwadratu
kwadratu 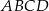 może zawierać się w prostej o równaniu
może zawierać się w prostej o równaniu
A) 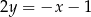 B)
B) 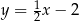 C)
C) 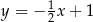 D)
D) 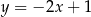
Jeżeli 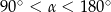 oraz
oraz 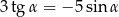 , to
, to
A) 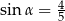 B)
B) 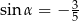 C)
C) 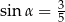 D)
D) 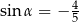
Wskaż liczbę, która spełnia równanie 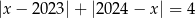 .
.
A) 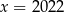 B)
B) 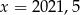 C)
C) 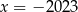 D)
D) 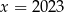
Cięciwy 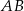 i
i 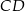 okręgu o środku
okręgu o środku 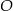 przecinają się w punkcie
przecinają się w punkcie 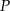 i tworzą trójkąty
i tworzą trójkąty 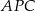 i
i 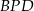 .
.
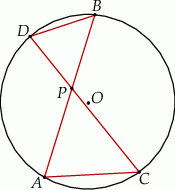
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1, 2 albo 3.
Trójkąty 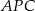 i
i 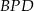 są
są
| A) podobne, | B) przystające, |
ponieważ trójkąty te mają równe
| 1) pola, | 2) miary kątów, | 3) długości boków, |
Dany jest trapez 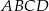 , w którym
, w którym 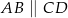 oraz przekątne
oraz przekątne 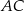 i
i 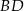 przecinają się w punkcie
przecinają się w punkcie 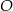 . Wysokość tego trapezu jest równa 15. Obwód trójkąta
. Wysokość tego trapezu jest równa 15. Obwód trójkąta 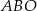 jest równy 42, a obwód trójkąta
jest równy 42, a obwód trójkąta 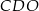 jest równy 14.
jest równy 14.
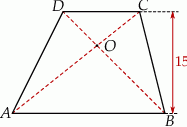
Wysokość trójkąta 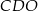 poprowadzona z punktu
poprowadzona z punktu 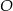 jest równa
jest równa
A) 3,75 B) 5 C) 6 D) 7,5
Informacja do zadań 25.1 i 25.2
W grupie 320 respondentów przeprowadzono ankietę, w której zapytano o liczbę wysłanych przez nich wiadomości e-mail pomiędzy 1 a 6 marca. Wyniki ankiety zebrano w poniższej tabeli.
| Liczba e-maili | 10 | 20 | 30 | 40 | 50 | 60 |
| Liczba osób | 53 | 93 | 28 | 75 | 44 | 27 |
Średnia liczba wiadomości e-mail wysłanych dziennie przez jedną osobę uczestniczącą w badaniu, jest z dokładnością do jednej wiadomości równa
A) 5 B) 10 C) 4 D) 6
Mediana danych przedstawionych w tabeli jest równa
A) 20 B) 25 C) 30 D) 35
Dany jest ostrosłup prawidłowy trójkątny 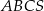 o podstawie
o podstawie 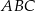 . Punkty
. Punkty 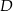 ,
, 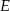 i
i 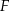 są punktami – odpowiednio – krawędzi bocznych
są punktami – odpowiednio – krawędzi bocznych 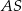 ,
, 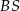 i
i 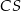 takimi, że
takimi, że 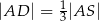 ,
, 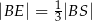 i
i 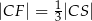 (zobacz rysunek).
(zobacz rysunek).
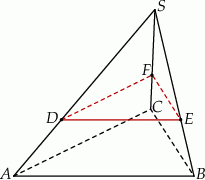
Stosunek objętości ostrosłupa 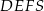 do objętości ostrosłupa
do objętości ostrosłupa 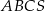 jest równy
jest równy
A) 8 : 27 B) 2 : 3 C) 8 : 9 D) 4 : 9
Boki równoległoboku mają długości 6 i 14, a jego krótsza przekątna ma długość 11. Oblicz cosinus kąta rozwartego tego równoległoboku.
Sprzedawca kupuje miesięcznie w hurtowni monitory, płacąc 1920 zł za sztukę. W chwili obecnej sprzedaje 20 monitorów miesięcznie w cenie 2240 zł za sztukę, oraz oszacował, że każda kolejna obniżka ceny o 16 zł zwiększa o 2 liczbę sprzedanych monitorów. Jaką powinien ustalić cenę monitora, aby jego zysk był największy? Ile jest równy ten maksymalny miesięczny zysk?
Dane są czworościany foremne: czworościan 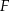 o krawędzi długości
o krawędzi długości 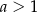 , czworościan
, czworościan 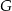 o krawędzi długości
o krawędzi długości 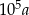 i czworościan
i czworościan 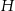 o krawędzi długości
o krawędzi długości 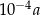 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Objętość czworościanu 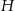 jest jest 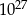 razy mniejsza od objętości czworościanu razy mniejsza od objętości czworościanu 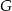 . . | P | F |
Iloczyn długości krawędzi czworościanów 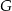 i i 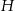 jest 10 razy większa od długości krawędzi czworościanu jest 10 razy większa od długości krawędzi czworościanu 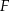 . . | P | F |
Ze zbioru liczb naturalnych dwucyfrowych losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że w zapisie dziesiętnym wylosowanej liczby jest dokładnie jedna cyfra 3?
A) 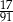 B)
B) 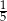 C)
C) 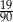 D)
D)