/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 10 kwietnia 2010 Czas pracy: 180 minut
Dwa pociągi: towarowy o długości 490 m i osobowy o długości 210 m, jadą naprzeciw siebie po dwóch równoległych torach i spotykają się w miejscu  . Mijanie się pociągów trwa 20 s, a czas przejazdu pociągu osobowego przez miejsce
. Mijanie się pociągów trwa 20 s, a czas przejazdu pociągu osobowego przez miejsce 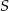 jest o 25 sekund krótszy od czasu przejazdu pociągu towarowego. Oblicz prędkości obu pociągów, zakładając, że poruszają się ruchem jednostajnym.
jest o 25 sekund krótszy od czasu przejazdu pociągu towarowego. Oblicz prędkości obu pociągów, zakładając, że poruszają się ruchem jednostajnym.
Wyznacz dziedzinę funkcji
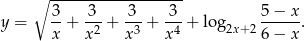
W trójkącie prostokątnym 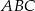 wysokość
wysokość 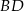 dzieli przeciwprostokątną
dzieli przeciwprostokątną 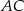 na odcinki o długościach
na odcinki o długościach 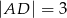 i
i 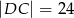 .
.
- Oblicz długości boków trójkąta
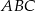 .
. - Oblicz długość odcinka
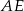 , gdzie
, gdzie 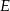 jest punktem wspólnym dwusiecznej kąta
jest punktem wspólnym dwusiecznej kąta 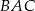 i boku
i boku 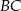 .
.
Dane są dwa nieskończone ciągi 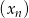 i
i 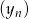 takie, że dla każdego
takie, że dla każdego 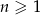 , punkt o współrzędnych
, punkt o współrzędnych 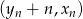 jest środkiem ciężkości trójkąta o wierzchołkach
jest środkiem ciężkości trójkąta o wierzchołkach 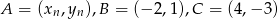 . Wyznacz wzory ciągów
. Wyznacz wzory ciągów 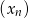 i
i 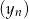 .
.
Prawdopodobieństwa zdarzeń 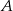 i
i 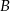 oraz zdarzeń do nich przeciwnych spełniają warunki:
oraz zdarzeń do nich przeciwnych spełniają warunki: 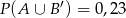 i
i 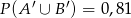 .
.
- Oblicz
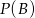 .
. - Wykaż, że jeżeli
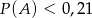 to
to 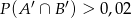 .
.
- Wykaż, że równanie
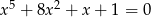 nie ma rozwiązań w przedziale
nie ma rozwiązań w przedziale 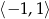 .
. - Wykaż, że równanie
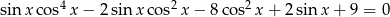
nie ma rozwiązań rzeczywistych.
Środki okręgów 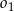 i
i 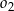 znajdują się po różnych stronach prostej
znajdują się po różnych stronach prostej 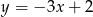 , która zawiera punkty wspólne tych okręgów. Wiedząc, że promień okręgu
, która zawiera punkty wspólne tych okręgów. Wiedząc, że promień okręgu 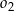 jest równy
jest równy 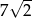 oraz, że okrąg
oraz, że okrąg 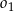 ma równanie
ma równanie 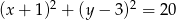 , wyznacz równanie okręgu
, wyznacz równanie okręgu 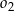 .
.
Proste 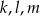 są parami różne i równoległe. Na prostych tych wybrano zbiór
są parami różne i równoległe. Na prostych tych wybrano zbiór 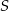 składający się z
składający się z 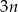 punktów (
punktów (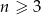 ), przy czym na każdej z prostych wybrano
), przy czym na każdej z prostych wybrano  punktów. Wiadomo ponadto, że jeżeli trzy punkty zbioru
punktów. Wiadomo ponadto, że jeżeli trzy punkty zbioru 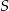 leżą na jednej prostej, to prostą tą jest
leżą na jednej prostej, to prostą tą jest 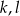 lub
lub 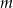 . Oblicz ile jest trójkątów o wierzchołkach należących do zbioru
. Oblicz ile jest trójkątów o wierzchołkach należących do zbioru 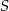 .
.
Wszystkie krawędzie boczne ostrosłupa trójkątnego 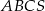 o wierzchołku
o wierzchołku 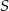 mają długość
mają długość 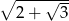 . Wiedząc, że
. Wiedząc, że 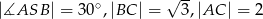 oblicz objętość tego ostrosłupa.
oblicz objętość tego ostrosłupa.
Wyznacz wszystkie wartości parametru 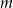 , dla których jeden z pierwiastków równania
, dla których jeden z pierwiastków równania
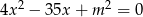
jest kwadratem drugiego pierwiastka. Oblicz te pierwiastki.

