/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 24 kwietnia 2021 Czas pracy: 180 minut
Zadania zamknięte
Wielomian 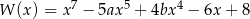 jest podzielny przez wielomian
jest podzielny przez wielomian 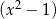 . Zatem
. Zatem
A) 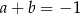 . B)
. B) 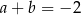 . C)
. C) 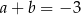 . D)
. D) 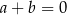 .
.
Prosta 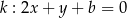 ma dwa punkty wspólne z parabolą
ma dwa punkty wspólne z parabolą 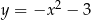 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
A) 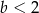 B)
B) 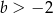 C)
C) 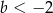 D)
D) 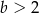
Wyrażenie 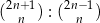 dla liczby naturalnej
dla liczby naturalnej 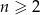 jest równe
jest równe
A) 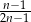 B)
B) 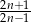 C) 2 D)
C) 2 D) 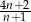
Rozwiązaniem nierówności 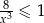 jest zbiór
jest zbiór
A) 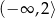 B)
B) 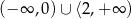 C)
C) 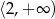 D)
D) 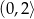
Zadania otwarte
W trójkącie 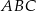 bok
bok 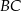 jest 3 razy krótszy od boku
jest 3 razy krótszy od boku 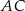 , a długość boku
, a długość boku 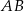 stanowi
stanowi 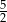 długości boku
długości boku 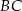 . Oblicz cosinus największego kąta trójkąta
. Oblicz cosinus największego kąta trójkąta 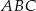 .
.
Z punktu 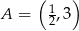 poprowadzono styczne do wykresu funkcji
poprowadzono styczne do wykresu funkcji 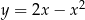 . Wyznacz równia tych stycznych.
. Wyznacz równia tych stycznych.
Dana jest liczba 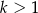 . Wyrazy ciągu
. Wyrazy ciągu 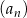 , określonego dla
, określonego dla 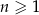 , spełniają warunki
, spełniają warunki
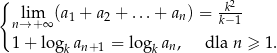
Udowodnij, że
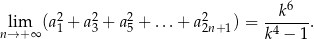
Wiadomo, że 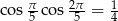 . Udowodnij, że przekątna pięciokąta foremnego o boku długości 1 ma długość
. Udowodnij, że przekątna pięciokąta foremnego o boku długości 1 ma długość 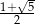 .
.
Każda krawędź graniastosłupa prawidłowego trójkątnego  ma długość 4 (zobacz rysunek).
ma długość 4 (zobacz rysunek).
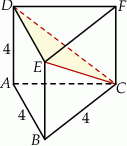
Oblicz odległość wierzchołka 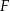 tego graniastosłupa od płaszczyzny
tego graniastosłupa od płaszczyzny 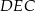 .
.
Rozwiąż równanie
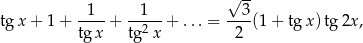
w którym lewa strona jest sumą wyrazów nieskończonego ciągu geometrycznego.
Oblicz, ile jest wszystkich ośmiocyfrowych liczb naturalnych, w których zapisie dziesiętnym występują dokładnie cztery cyfry 4 i dokładnie dwie cyfry 2.
Wyznacz wszystkie wartości parametru 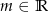 , dla których pierwiastki wielomianu
, dla których pierwiastki wielomianu 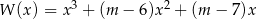 tworzą ciąg arytmetyczny.
tworzą ciąg arytmetyczny.
Jeden bok kwadratu opisanego okręgu o równaniu 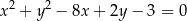 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 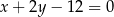 . Oblicz współrzędne wierzchołków tego kwadratu.
. Oblicz współrzędne wierzchołków tego kwadratu.
W pudełku znajduje się 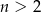 sześciennych kostek do gry, przy czym
sześciennych kostek do gry, przy czym 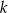 spośród tych kostek (
spośród tych kostek (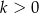 i
i 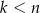 ) ma na dwóch ściankach jedno oczko, a na pozostałych czterech ściankach sześć oczek. Wybieramy losowo jedną z tych kostek i wykonujemy nią cztery kolejne rzuty. Oblicz jakie jest prawdopodobieństwo, że wybrana kostka miała jedno oczko na dwóch ściankach, jeżeli wiadomo, że w każdym z czterech wykonanych rzutów otrzymano ściankę z sześcioma oczkami.
) ma na dwóch ściankach jedno oczko, a na pozostałych czterech ściankach sześć oczek. Wybieramy losowo jedną z tych kostek i wykonujemy nią cztery kolejne rzuty. Oblicz jakie jest prawdopodobieństwo, że wybrana kostka miała jedno oczko na dwóch ściankach, jeżeli wiadomo, że w każdym z czterech wykonanych rzutów otrzymano ściankę z sześcioma oczkami.
Z arkusza blachy w kształcie półkola o promieniu 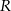 należy wyciąć trapez, którego jedna podstawa jest średnicą tego półkola, a wierzchołki drugiej podstawy leżą na jego brzegu (zobacz rysunek).
należy wyciąć trapez, którego jedna podstawa jest średnicą tego półkola, a wierzchołki drugiej podstawy leżą na jego brzegu (zobacz rysunek).
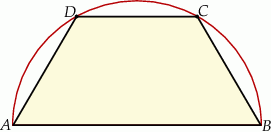
Oblicz jaką długość powinno mieć ramię tego trapezu, aby jego pole było największe możliwe. Oblicz to pole.

