/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 14 marca 2020 Czas pracy: 180 minut
Zadania zamknięte
Dla dowolnych liczb 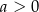 ,
, 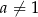 ,
, 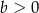 ,
, 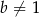 ,
, 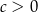 ,
, 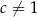 wartość wyrażenia
wartość wyrażenia
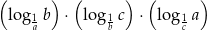
jest równa
A) 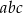 B)
B) 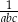 C)
C) 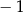 D) 1
D) 1
Zbiorem wartości funkcji 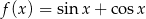 , gdzie
, gdzie 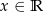 , jest przedział
, jest przedział
A) 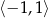 B)
B) 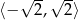 C)
C) 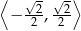 D)
D) 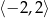
Wiadomo, że wielomian 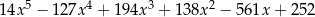 ma w zbiorze
ma w zbiorze 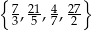 dokładnie jeden pierwiastek wymierny. Jest nim liczba
dokładnie jeden pierwiastek wymierny. Jest nim liczba
A)  B)
B) 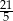 C)
C) 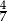 D)
D) 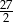
Granica 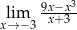 jest równa
jest równa
A) 0 B) 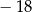 C)
C) 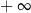 D)
D) 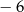
W okrąg o równaniu 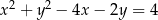 wpisano trójkąt równoramienny, w którym ramię tworzy z podstawą kąt o mierze
wpisano trójkąt równoramienny, w którym ramię tworzy z podstawą kąt o mierze 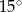 . Podstawa tego trójkąta ma długość
. Podstawa tego trójkąta ma długość
A) 1,5 B) 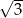 C) 3 D)
C) 3 D) 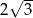
Zadania otwarte
Styczna do paraboli o równaniu 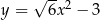 w punkcie
w punkcie 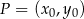 jest nachylona do osi
jest nachylona do osi 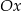 pod kątem
pod kątem 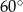 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 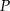 .
.
Oblicz sumę nieskończonego szeregu geometrycznego
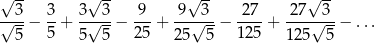
Udowodnij, że jeżeli 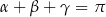 , to
, to
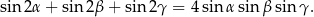
Dany jest trójkąt równoramienny 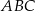 , w którym
, w którym 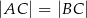 . Na ramieniu
. Na ramieniu 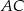 tego trójkąta wybrano punkt
tego trójkąta wybrano punkt 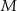 (
(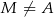 i
i 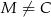 ), a na ramieniu
), a na ramieniu 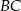 wybrano punkt
wybrano punkt 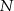 . Przez punkty
. Przez punkty 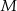 i
i 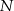 poprowadzono proste prostopadłe do podstawy
poprowadzono proste prostopadłe do podstawy 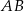 tego trójkąta, które wyznaczają na niej punkty
tego trójkąta, które wyznaczają na niej punkty 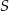 i
i 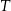 . Wykaż, że jeżeli
. Wykaż, że jeżeli 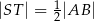 , to
, to 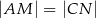 .
.
Dana jest funkcja 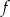 określona wzorem
określona wzorem 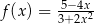 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  , oraz dwie liczby:
, oraz dwie liczby: 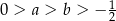 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
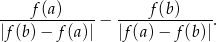
Liczby 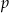 i
i 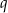 są pierwiastkami równania
są pierwiastkami równania 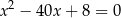 . Wykaż, że wartość wyrażenia
. Wykaż, że wartość wyrażenia 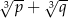 jest liczbą naturalną.
jest liczbą naturalną.
Doświadczenie losowe polega na tym, że losujemy bez zwracania trzy liczby ze zbioru 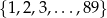 . Oblicz prawdopodobieństwo, że wśród wylosowanych liczb jest liczba parzysta, jeżeli wiadomo, że pierwsza z wylosowanych liczb jest nieparzysta.
. Oblicz prawdopodobieństwo, że wśród wylosowanych liczb jest liczba parzysta, jeżeli wiadomo, że pierwsza z wylosowanych liczb jest nieparzysta.
Obrazem trójkąta 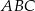 w jednokładności o środku
w jednokładności o środku 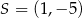 i skali
i skali 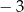 jest trójkąt
jest trójkąt 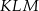 o wierzchołkach
o wierzchołkach 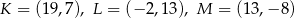 . Wyznacz współrzędne wierzchołków trójkąta
. Wyznacz współrzędne wierzchołków trójkąta 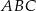 .
.
Podstawą ostrosłupa prawidłowego 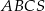 jest trójkąt równoboczny
jest trójkąt równoboczny 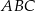 o boku długości 8. Na krawędziach bocznych
o boku długości 8. Na krawędziach bocznych 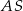 i
i 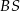 wybrano punkty, odpowiednio
wybrano punkty, odpowiednio 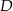 i
i 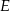 , takie że
, takie że 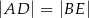 oraz
oraz 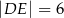 (zobacz rysunek). Płaszczyzna
(zobacz rysunek). Płaszczyzna 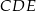 jest prostopadła do płaszczyzny ściany bocznej
jest prostopadła do płaszczyzny ściany bocznej  ostrosłupa.
ostrosłupa.
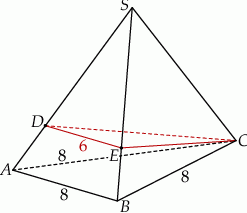
Oblicz objętość tego ostrosłupa.
Reszta z dzielenia wielomianu 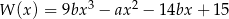 przez trójmian
przez trójmian 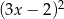 wynosi 3. Oblicz
wynosi 3. Oblicz  i
i 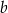 . Dla wyznaczonych wartości
. Dla wyznaczonych wartości  i
i 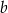 rozwiąż nierówność
rozwiąż nierówność 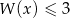 .
.
Rozpatrujemy wszystkie trójkąty równoramienne o ramionach długości 6. Oblicz cosinus kąta między ramionami tego z tych trójkątów, dla którego objętość bryły powstałej w wyniku obrotu trójkąta dokoła prostej zawierającej jego podstawę jest największa możliwa. Oblicz tę największą objętość.

