/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 30 kwietnia 2022 Czas pracy: 180 minut
Zadania zamknięte
Liczba 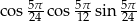 jest równa
jest równa
A) 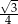 B)
B)  C)
C) 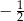 D)
D) 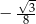
Rysunek przedstawia wykres funkcji 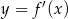 .
.
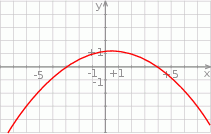
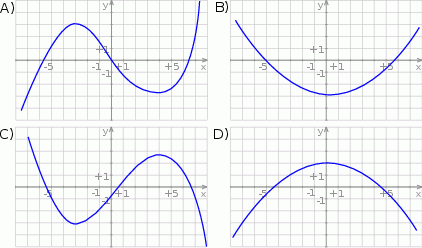
Wskaż wykres funkcji 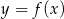 .
.
Wielomian 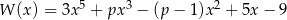 jest podzielny przez dwumian
jest podzielny przez dwumian 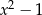 dla
dla 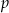 równego
równego
A) 6 B) 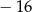 C) 4 D)
C) 4 D) 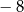
Na rysunku przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność 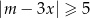 .
.
![]()
Stąd wynika, że
A) 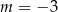 B)
B) 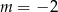 C)
C) 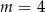 D)
D) 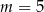
Zadania otwarte
Oblicz granicę jednostronną funkcji 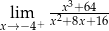 .
.
Wykaż, że dla dowolnych liczb rzeczywistych  i
i 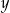 takich, że
takich, że 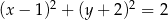 , prawdziwa jest nierówność
, prawdziwa jest nierówność 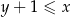 .
.
Wyznacz wzór funkcji kwadratowej 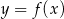 wiedząc, że jest on styczny do prostej
wiedząc, że jest on styczny do prostej 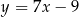 w punkcie
w punkcie 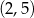 oraz przechodzi przez punkt
oraz przechodzi przez punkt 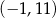 .
.
Pole trapezu równoramiennego opisanego na okręgu jest równe 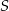 , a kąt ostry przy podstawie ma miarę
, a kąt ostry przy podstawie ma miarę  . Wykaż, że ramię tego trapezu ma długość
. Wykaż, że ramię tego trapezu ma długość 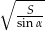 .
.
W pudełku znajdują się 4 kostki do gry: 3 sześcienne (ze ścianami ponumerowanymi liczbami od 1 do 6) i jedna czworościenna (ze ścianami ponumerowanymi liczbami od 1 do 4). Losowo wybrano kostkę, wykonano nią 3 rzuty i w wyniku tych 3 rzutów otrzymano trzy razy jedynkę. Jakie jest prawdopodobieństwo, że wybrana kostka była kostką czworościenną?
Liczba 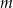 jest sumą odwrotności dwóch różnych pierwiastków równania
jest sumą odwrotności dwóch różnych pierwiastków równania
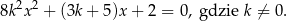
Wyznacz zbiór wartości funkcji określonej wzorem 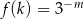 .
.
Wyznacz wszystkie wartości parametru  , dla których wykresy funkcji
, dla których wykresy funkcji 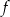 i
i 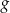 , określonych wzorami
, określonych wzorami 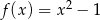 oraz
oraz 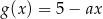 , przecinają w dwóch punktach znajdujących się powyżej osi
, przecinają w dwóch punktach znajdujących się powyżej osi 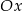 układu współrzędnych.
układu współrzędnych.
Rozwiąż równanie 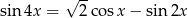 w przedziale
w przedziale 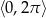 .
.
W ostrosłup prawidłowy czworokątny wpisano sześcian tak, że jego cztery wierzchołki należą do wysokości ścian bocznych ostrosłupa, a pozostałe do płaszczyzny podstawy. Oblicz stosunek objętości ostrosłupa do objętości sześcianu jeżeli kąt nachylenia ściany bocznej do płaszczyzny podstawy jest równy  .
.
Punkt 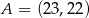 jest wierzchołkiem trójkąta prostokątnego o polu
jest wierzchołkiem trójkąta prostokątnego o polu 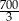 . Prosta
. Prosta 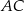 zawiera przeciwprostokątną tego trójkąta, a prosta zwierająca przyprostokątną
zawiera przeciwprostokątną tego trójkąta, a prosta zwierająca przyprostokątną 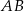 ma równanie
ma równanie 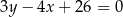 . Środek okręgu wpisanego w trójkąt
. Środek okręgu wpisanego w trójkąt 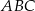 ma współrzędne
ma współrzędne 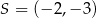 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 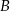 i
i 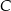 tego trójkąta.
tego trójkąta.
Na rysunku poniżej przedstawiono fragment wykresu funkcji 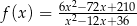 określonej dla
określonej dla 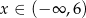 . Wykres ten przecina osie
. Wykres ten przecina osie 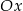 i
i 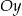 odpowiednio w punktach
odpowiednio w punktach 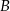 i
i 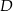 , a punkt
, a punkt 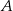 jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty
jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty 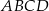 , w których punkt
, w których punkt 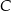 leży na wykresie funkcji
leży na wykresie funkcji 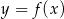 pomiędzy punktami
pomiędzy punktami 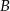 i
i 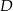 .
.
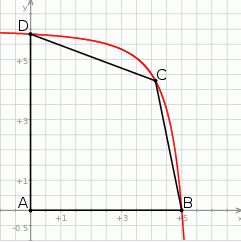
Oblicz pierwszą współrzędną wierzchołka 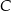 tego z rozpatrywanych czworokątów, którego pole jest największe.
tego z rozpatrywanych czworokątów, którego pole jest największe.

