/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny/Czworokątny

Zadanie nr 6461116

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą ostrosłupa 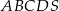ABCDS jest prostokąt 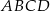ABCD , w którym 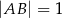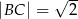|AB | = 1 , √ -- |BC | = 2 . Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz cosinus kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.

Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

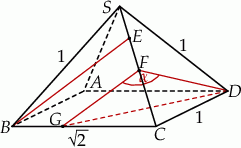
Zauważmy, że trójkąt 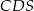CDS jest równoboczny, a trójkąt 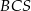BCS prostokątny (jest to połówka kwadratu). Najtrudniejsze w tym zadaniu to odpowiednio narysować płaszczyznę, w której będziemy liczyć miarę kąta między ścianami. Płaszczyzna ta musi być prostopadła do krawędzi kąta, w dodatku możemy tak ją wybrać, żeby przechodziła przez punkt 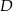D . W otrzymanym trójkącie 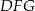DF G znamy długość boku 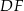DF (wysokość w trójkącie równobocznym)

√ -- --3- DF = 2 .

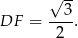
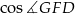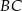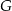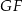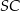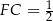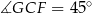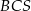Aby obliczyć pozostałe boki (liczymy je, żeby z twierdzenia cosinusów obliczyć cos∡GF D ) musimy ustalić, gdzie na boku BC leży punkt G . To co wiemy, to że odcinek GF jest prostopadły do krawędzi SC oraz 1 FC = 2 . Jak wcześniej zauważyliśmy, ∘ ∡GCF = 45 (bo BCS jest równoramiennym trójkątem prostokątnym). Zatem 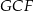GCF jest równoramiennym trójkątem prostokątnym, czyli

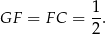
1- GF = FC = 2 .

Ponadto 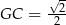√- GC = 22- , więc z trójkąta prostokątnego 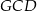GCD mamy

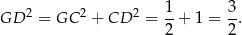
GD 2 = GC 2 + CD 2 = 1-+ 1 = 3. 2 2

Stosujemy teraz twierdzenie cosinusów w trójkącie 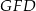GF D .

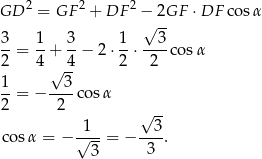
GD 2 = GF 2 + DF 2 − 2GF ⋅ DF cos α √ -- 3-= 1-+ 3-− 2 ⋅ 1-⋅--3co sα 2 4 √ 4- 2 2 1 3 --= − ----cosα 2 2 √ -- √1-- --3- cos α = − 3 = − 3 .

 
Odpowiedź: √ - --3 − 3

Wersja PDF
Rozwiązanie Losuj ponownie