Zadanie nr 3142537
Odcinek 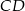 jest zawarty w dwusiecznej kąta
jest zawarty w dwusiecznej kąta 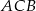 trójkąta
trójkąta 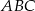 . Kąty trójkąta
. Kąty trójkąta 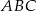 mają miary
mają miary 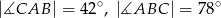 . Styczna do okręgu opisanego na tym trójkącie w punkcie
. Styczna do okręgu opisanego na tym trójkącie w punkcie 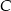 przecina prostą
przecina prostą 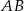 w punkcie
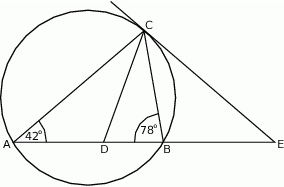
w punkcie 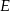 (zobacz rysunek). Oblicz, ile stopni ma każdy z kątów trójkąta
(zobacz rysunek). Oblicz, ile stopni ma każdy z kątów trójkąta 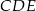 .
.
Rozwiązanie
Sposób I
Na mocy twierdzenia o stycznej mamy
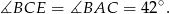
Ponadto, patrząc na trójkąt 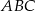 mamy
mamy
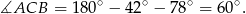
Zatem
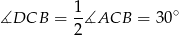
oraz
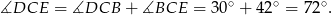
Z trójkąta 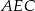 mamy
mamy
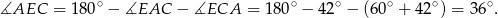
Teraz patrzymy na trójkąt 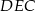
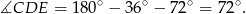
Sposób II
Jeżeli nie chcemy korzystać z twierdzenia o stycznej i siecznej, dorysujmy środek okręgu 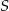 i promienie
i promienie 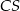 i
i 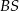 .
.
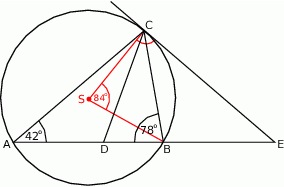
Ponieważ kąt środkowy jest dwa razy większy od kąta wpisanego opartego na tym samym łuku, mamy
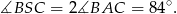
Trójkąt 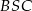 jest równoramienny więc
jest równoramienny więc
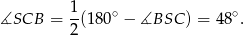
Teraz korzystamy z tego, że promień okręgu 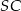 jest prostopadły do stycznej przechodzącej przez punkt
jest prostopadły do stycznej przechodzącej przez punkt 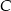 . Mamy więc
. Mamy więc
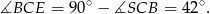
Resztę kątów wyliczamy tak samo jak w I sposobie.
Odpowiedź: