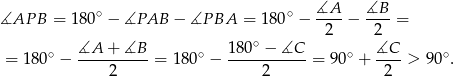Zadanie nr 4964484
W trójkącie 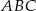 poprowadzono dwusieczne kątów
poprowadzono dwusieczne kątów 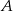 i
i 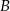 . Dwusieczne te przecinają się w punkcie
. Dwusieczne te przecinają się w punkcie 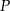 . Uzasadnij, że kąt
. Uzasadnij, że kąt 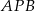 jest rozwarty.
jest rozwarty.
Rozwiązanie
Rozpoczynamy od rysunku.
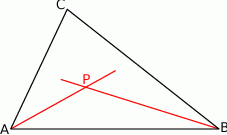
Obliczamy miarę kąta 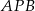 .
.
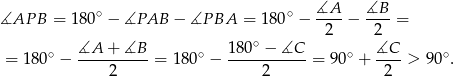
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie 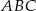 poprowadzono dwusieczne kątów
poprowadzono dwusieczne kątów 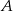 i
i 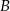 . Dwusieczne te przecinają się w punkcie
. Dwusieczne te przecinają się w punkcie 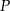 . Uzasadnij, że kąt
. Uzasadnij, że kąt 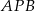 jest rozwarty.
jest rozwarty.
Rozpoczynamy od rysunku.

Obliczamy miarę kąta 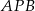 .
.