Zadanie nr 7873550
Oblicz pole czworokąta wypukłego 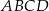 , w którym kąty wewnętrzne mają odpowiednio miary:
, w którym kąty wewnętrzne mają odpowiednio miary: 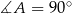 ,
, 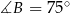 ,
, 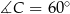 ,
, 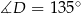 , a boki
, a boki 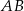 i
i 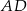 mają długość 3 cm. Sporządź rysunek pomocniczy.
mają długość 3 cm. Sporządź rysunek pomocniczy.
Rozwiązanie
Zróbmy najpierw rysunek pomocniczy.
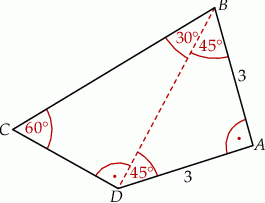
Trójkąt 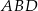 jest równoramienny i prostokątny, zatem jego kąty przy wierzchołkach
jest równoramienny i prostokątny, zatem jego kąty przy wierzchołkach 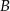 i
i 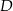 są równe 45
są równe 45 . W połączeniu z podanymi w treści zadania miarami kątów, daje to nam:
. W połączeniu z podanymi w treści zadania miarami kątów, daje to nam: 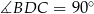 oraz
oraz 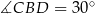 . Pole trójkąta
. Pole trójkąta 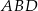 jest równe:
jest równe:
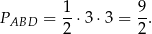
Pozostaje zatem obliczyć pole drugiego trójkąta - 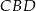 . Aby to zrobić musimy obliczyć długości jego przyprostokątnych. Jedna z nich to przeciwprostokątna trójkąta
. Aby to zrobić musimy obliczyć długości jego przyprostokątnych. Jedna z nich to przeciwprostokątna trójkąta 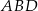 – obliczymy ją z twierdzenia Pitagorasa, drugą obliczymy z funkcji trygonometrycznych w trójkącie
– obliczymy ją z twierdzenia Pitagorasa, drugą obliczymy z funkcji trygonometrycznych w trójkącie 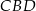 .
.
Liczymy 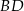 :
:
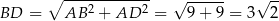
Aby obliczyć 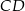 , zauważmy, że
, zauważmy, że 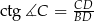 . Mamy stąd:
. Mamy stąd:
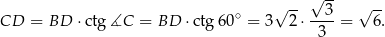
Bez trudu obliczamy teraz pole czworokąta  :
:
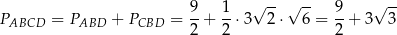
Odpowiedź: