Wysokość 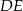 rombu
rombu 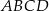 dzieli bok
dzieli bok 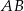 tego rombu tak, że
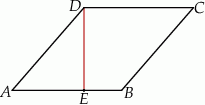
tego rombu tak, że 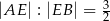 (zobacz rysunek).
(zobacz rysunek).
Oblicz wartość wyrażenia
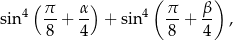
gdzie  i
i 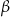 są dwoma sąsiednimi kątami wewnętrznymi rombu
są dwoma sąsiednimi kątami wewnętrznymi rombu  .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wysokość 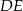 rombu
rombu 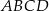 dzieli bok
dzieli bok  tego rombu tak, że
tego rombu tak, że 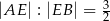 (zobacz rysunek).
(zobacz rysunek).

Oblicz wartość wyrażenia
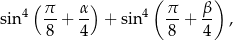
gdzie  i
i 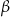 są dwoma sąsiednimi kątami wewnętrznymi rombu
są dwoma sąsiednimi kątami wewnętrznymi rombu  .
.
Na bokach 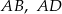 i
i 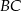 rombu
rombu 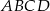 wybrano odpowiednio punkty
wybrano odpowiednio punkty 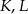 i
i 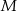 w ten sposób, że odcinki
w ten sposób, że odcinki 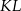 i
i 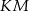 są równoległe do przekątnych rombu. Wykaż, że odcinek
są równoległe do przekątnych rombu. Wykaż, że odcinek 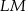 przechodzi przez punkt przecięcia przekątnych rombu.
przechodzi przez punkt przecięcia przekątnych rombu.
Kąt ostry rombu 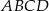 ma miarę
ma miarę 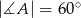 . Na bokach
. Na bokach 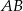 i
i 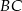 wybrano punkty
wybrano punkty 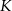 i
i 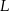 w ten sposób, że
w ten sposób, że 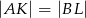 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 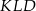 jest trójkątem równobocznym.
jest trójkątem równobocznym.
Oblicz długość boku rombu wiedząc, że prosta poprowadzona przez jeden z jego wierzchołków odcina na przedłużeniach dwóch jego boków odcinki o długościach 4 i 9.
Oblicz pole rombu 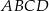 , wiedząc, że długości promieni okręgów opisanych na trójkątach
, wiedząc, że długości promieni okręgów opisanych na trójkątach 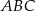 i
i 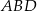 odpowiednio są równe
odpowiednio są równe 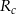 i
i 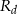 .
.
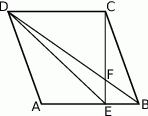
Przekątna 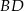 rombu
rombu 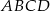 przecina jego wysokość
przecina jego wysokość 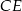 , poprowadzoną na bok
, poprowadzoną na bok 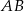 , w punkcie
, w punkcie 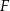 . Oblicz pole rombu
. Oblicz pole rombu 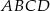 , jeśli wiadomo, że
, jeśli wiadomo, że 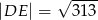 oraz
oraz 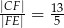 .
.