Zadanie nr 3605332
Rozpatrujemy wszystkie walce o danym polu powierzchni całkowitej 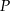 . Oblicz wysokość i promień podstawy tego walca, którego objętość jest największa. Oblicz tę największą objętość.
. Oblicz wysokość i promień podstawy tego walca, którego objętość jest największa. Oblicz tę największą objętość.
Rozwiązanie
Niech  i
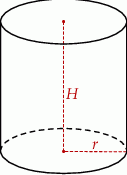
i 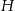 oznaczają odpowiednio promień podstawy i wysokość walca.
oznaczają odpowiednio promień podstawy i wysokość walca.
Z podanego pola powierzchni całkowitej mamy
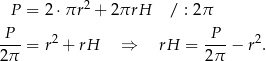
Liczymy objętość walca.
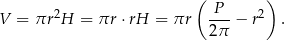
Aby wyznaczyć największą możliwą objętość walca liczymy pochodną funkcji
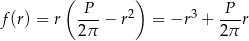
określonej dla 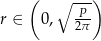 . Liczymy
. Liczymy
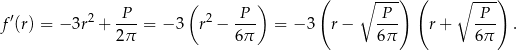
Wykresem pochodnej jest fragment paraboli o ramionach skierowanych w dół, więc pochodna jest dodatnia w przedziale 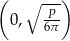 i ujemna w przedziale
i ujemna w przedziale 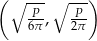 . To oznacza, że w punkcie
. To oznacza, że w punkcie 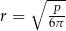 funkcja
funkcja 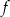 osiąga największą wartość. Objętość walca jest wtedy równa
osiąga największą wartość. Objętość walca jest wtedy równa
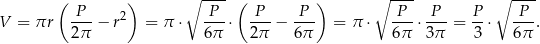
Wysokość walca jest wtedy równa
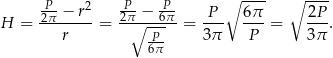
Odpowiedź: 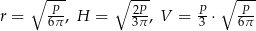 .
.

