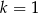/Szkoła średnia/Geometria/Planimetria/Zadania na ekstrema

Zadanie nr 1275676

Na bokach 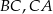BC ,CA i 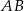trójkąta 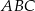ABC wybrano punkty 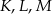K,L ,M takie, że

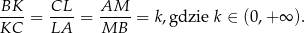
BK--= CL--= AM---= k,gdzie k ∈ (0,+ ∞ ). KC LA MB

Wyznacz wartość 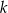, dla której stosunek pola trójkąta 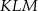KLM do pola trójkąta ABC jest najmniejszy.

Rozwiązanie

Szkicujemy opisaną sytuację.

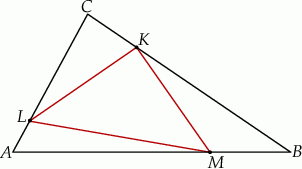
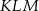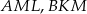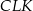Pole trójkąta KLM obliczamy odejmując od pola trójkąta ABC pola trójkątów AML ,BKM i CLK . Zauważmy najpierw, że z założenia 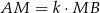AM = k ⋅MB , więc

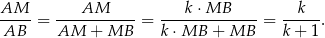
AM--- ----AM----- ---k-⋅MB------ --k--- AB = AM + MB = k⋅ MB + MB = k+ 1.

Podobnie

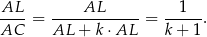
AL-- ----AL------ --1--- AC = AL + k⋅ AL = k + 1 .

Korzystamy teraz ze wzoru z sinusem.

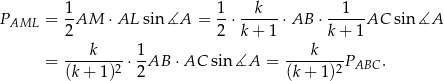
P = 1-AM ⋅AL sin∡A = 1-⋅ --k--⋅AB ⋅ --1--AC sin ∡A AML 2 2 k+ 1 k+ 1 k 1 k = -------2 ⋅--AB ⋅ AC sin ∡A = -------2PABC . (k + 1) 2 (k+ 1)

Analogicznie obliczamy

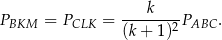
---k---- PBKM = PCLK = (k + 1 )2 PABC .

Mamy zatem

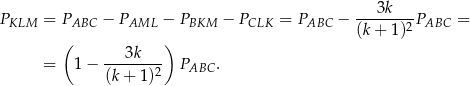
3k PKLM = PABC − PAML − PBKM − PCLK = PABC − -------2PABC = ( ) (k+ 1 ) ---3k--- = 1− (k + 1)2 PABC .

Zatem

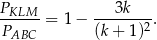
P 3k --KLM-= 1 − --------. PABC (k + 1)2

Liczymy pochodną otrzymanej funkcji

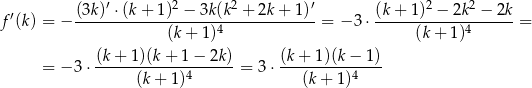
′ 2 2 ′ 2 2 f ′(k) = − (3k)-⋅(k-+-1)-−--3k(k-+--2k+--1)-= − 3⋅ (k+--1)-−--2k-−--2k = (k + 1)4 (k + 1)4 (k + 1)(k + 1 − 2k) (k+ 1)(k− 1) = − 3 ⋅------------------- = 3⋅ -------------- (k+ 1)4 (k+ 1)4

To oznacza, że pochodna jest ujemna na przedziale 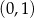(0,1) i dodatnia na przedziale 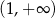(1 ,+∞ ) , czyli funkcja 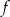jest malejąca na przedziale 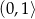(0,1⟩ i rosnąca na 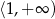⟨1,+ ∞ ) . Najmniejszy stosunek pól otrzymamy więc, gdy 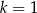k = 1 , czyli gdy punkty 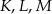K ,L,M są środkami boków.
Odpowiedź: k = 1

Rozwiązanie Losuj ponownie