Zadanie nr 3785612
Dany jest odcinek 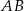 o długości 10. Rozpatrujemy wszystkie sześciokąty foremne
o długości 10. Rozpatrujemy wszystkie sześciokąty foremne 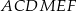 i trójkąty równoboczne
i trójkąty równoboczne 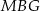 , których wspólny wierzchołek
, których wspólny wierzchołek 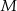 leży na odcinku
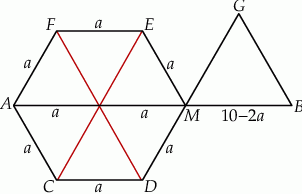
leży na odcinku 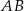 (zobacz rysunek).
(zobacz rysunek).
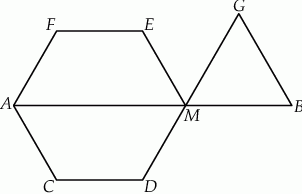
Oblicz stosunek obwodu sześciokąta 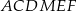 do obwodu trójkąta
do obwodu trójkąta 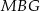 w przypadku, gdy suma pól tych dwóch wielokątów jest najmniejsza.
w przypadku, gdy suma pól tych dwóch wielokątów jest najmniejsza.
Rozwiązanie
Oznaczmy przez  bok sześciokąta foremnego
bok sześciokąta foremnego 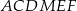 .
.
Ponieważ sześciokąt foremny składa się z 6 trójkątów równobocznych, 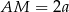 i
i 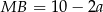 . Suma pól sześciokąta
. Suma pól sześciokąta 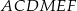 i trójkąta
i trójkąta 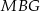 jest więc równa
jest więc równa
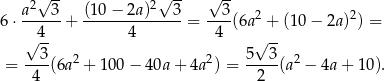
Dziedziną otrzymanej funkcji jest przedział 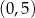 , a jej wykresem jest parabola o ramionach skierowanych w górę, więc najmniejszą sumę pól otrzymamy w wierzchołku, czyli dla
, a jej wykresem jest parabola o ramionach skierowanych w górę, więc najmniejszą sumę pól otrzymamy w wierzchołku, czyli dla
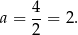
Stosunek obwodów tych figur jest wtedy równy
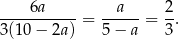
Odpowiedź: