Zadanie nr 2314180

Rozpatrujemy wszystkie trapezy równoramienne, w które można wpisać okrąg, spełniające warunek: suma długości dłuższej podstawy i wysokości trapezu jest równa 2.

Wyznacz wszystkie wartości , dla których istnieje trapez o podanych własnościach.
Wykaż, że obwód 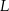takiego trapezu, jako funkcja długości dłuższej podstawy trapezu, wyraża się wzorem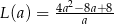
Oblicz tangens kąta ostrego tego spośród rozpatrywanych trapezów, którego obwód jest najmniejszy.

Rozwiązanie

Szkicujemy opisaną sytuację.

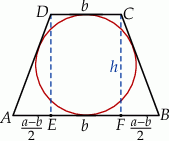
Oznaczmy tak jak w treści zdania 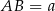AB = a . Wtedy 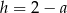h = 2 − a . Ponadto trapez jest opisany na okręgu, więc

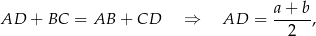
AD + BC = AB + CD ⇒ AD = a+--b, 2

gdzie 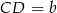CD = b jest długością krótszej podstawy trapezu.

Ponieważ 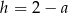, musi być 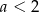. Z drugiej strony, 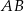ma być dłuższą podstawą trapezu, więc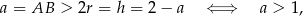
$a = AB > 2r = h = 2 − a ⇐ ⇒ a > 1,$

gdzie przez oznaczyliśmy promień okręgu wpisanego w trapez.
Odpowiedź: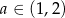
Obliczmy najpierw długość 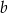krótszej podstawy trapezu – patrzymy na trójkąt prostokątny .
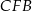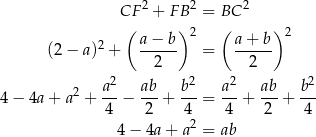
$2 2 2 CF + FB = BC ( a − b) 2 ( a + b) 2 (2 − a)2 + ------ = ------ 2 2 2 a2 ab b2 a2 ab b2 4− 4a+ a + ---− ---+ ---= ---+ ---+ --- 4 2 42 4 2 4 4− 4a+ a = ab$

Zatem 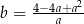i obwód trapezu jest równy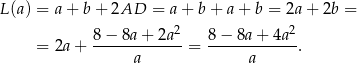

$L(a) = a+ b + 2AD = a + b + a + b = 2a + 2b = 8−--8a+--2a2- 8−--8a+--4a2- = 2a+ a = a .$
Liczymy pochodną funkcji
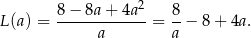
$2 L (a) = 8-−-8a-+-4a--= 8-− 8 + 4a. a a$

Jest ona równa

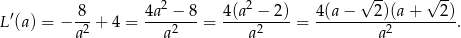
$2 2 √ -- √ -- L′(a) = − -8-+ 4 = 4a-−--8-= 4(a-−--2)-= 4(a-−---2-)(a-+---2-). a2 a2 a2 a2$

Widać teraz, że pochodna jest ujemna na przedziale 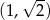i dodatnia na przedziale 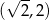. To oznacza, że 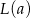maleje na przedziale 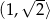i rośnie na przedziale 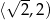. Najmniejszy obwód trapezu otrzymamy więc dla 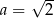. Wtedy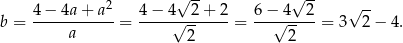

$2 √ -- √ -- √ -- b = 4-−-4a-+-a--= 4-−-4√--2-+-2-= 6−√-4--2-= 3 2− 4. a 2 2$

i interesujący nas tangens jest równy

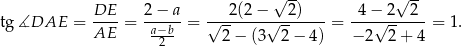
$√ -- √ -- tg∡DAE = DE--= 2−-a-= √--2(2-−√--2)----= -4-−√-2--2--= 1. AE a−b-- 2 − (3 2 − 4) − 2 2 + 4 2$

Odpowiedź: 1