Zadanie nr 1791104
Dane jest równanie 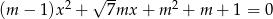 z niewiadomą
z niewiadomą  . Sporządź wykres funkcji
. Sporządź wykres funkcji 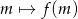 , gdzie
, gdzie 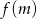 oznacza liczbę rzeczywistych pierwiastków danego równania.
oznacza liczbę rzeczywistych pierwiastków danego równania.
Rozwiązanie
Jeżeli 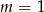 to mamy równanie
to mamy równanie 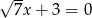 , które ma jedno rozwiązanie.
, które ma jedno rozwiązanie.
Jeżeli równanie jest kwadratowe, to liczymy 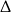 -ę.
-ę.
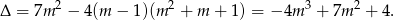
Musimy rozłożyć otrzymany wielomian. Szukamy najpierw pierwiastków całkowitych wśród dzielników wyrazu wolnego. Chwilę kombinując można znaleźć pierwiastek 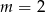 . Dzielimy wielomian przez
. Dzielimy wielomian przez 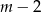 – my zrobimy to grupując wyrazy.
– my zrobimy to grupując wyrazy.
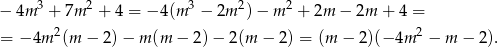
Łatwo sprawdzić, że trójmian w nawiasie nie ma pierwiastków, jest więc zawsze ujemny. Zatem
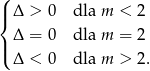
Uwzględniając fakt, że dla 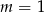 mamy równanie liniowe, dane równanie ma następującą liczbę rozwiązań
mamy równanie liniowe, dane równanie ma następującą liczbę rozwiązań
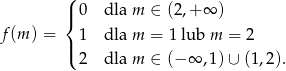
Pozostało naszkicować wykres funkcji 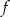 .
.